みんな苦手な因数分解、徹底解説します！
因数分解って苦手なんだよね…そんな悩みを持つ方はたくさんいますよね。
中学で習った因数分解以外にも、高校ではもっと応用的な因数分解も学習します。
他の単元での計算にも使用される重要な単元なので、今回は詳しく解説していきます。
Contents
因数分解とは？
因数分解は展開の逆？
まず、因数分解とは何か、ちゃんと理解していますか？
因数分解とは和の形を積の形に戻すことです。
例えば
のように積の形に直します。
では、展開とは何か、わかりますか？
展開は逆に計算できなくなるまで和の式で表すことです。
上の式で因数分解した式を計算すると
となります。
この２つの式を見比べてみると、因数分解は展開の逆の計算、展開は因数分解の逆の計算になっていることがわかります。
因数分解をする意味は？
因数分解はややこしいのに、なんでこんな計算するんだろう。そんな疑問を持つ人もいるかと思います。
因数分解が役に立つ！と実感するのは二次方程式、三次方程式を解く時です。
他の単元での計算でも求められるので難しそう…と先入観を持つのではなくこの場でマスターしてしまいましょう！
中学の復習！基本的な因数分解のやり方
まずは中学で習った基本的な因数分解の公式について復習していきましょう。
【例】
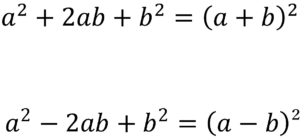
【例】
着目するポイントとしては一番最後の項が2乗になっていることです。この時、この公式を疑って他の項が条件を満たしているのかを確認します。
この場合は、
①４は２の2乗であるので
に当てはまるのかを疑う
②公式の2abを計算してみると
③公式に当てはまるので因数分解！
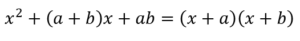
この形が一番スタンダードな形でよく使います。
3番目の項が積になるかつ2番目の項が和になる場合を考えます。
【例】
①積が16になるのは1×16、2×8、4×4の3パターン
②この中で和が10になるのは2と8の組み合わせ
③因数分解して答えは
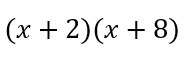
高校の因数分解はもっと難しい！？
高校の因数分解はこれだけで全部解けるわけではありません。
次は高校で追加される重要事項「たすき掛け」について学んでいきましょう。
たすきがけ
たすき掛けはいつ使うの？
今までは
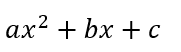
においてa=1の場合の因数分解について学んできました。
次はa≠1の場合について考えていきましょう。
この場合は「係数」と「定数項」に着目して「たすき掛け」が適用できないか？という選択肢が新たに加わります。
慣れないうちは計算に時間がかかってしまうかもしれませんが繰り返し練習していきましょう。
たすき掛けのやり方
基本的には3ステップで計算していきます。
①係数と定数項に着目する
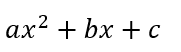
②かけ合わせてaになる2つの数…⑴、かけ合わせてcになる2つの数…⑵を考える
⑴⑵の組み合わせを考えて書き出す
③たすき掛けした和がbと等しくなる組み合わせを考えて因数分解する
この説明だけでは？？？となっている人がほとんどだと思うので、具体的な数字で計算していきましょう。
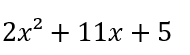
まずは積が2になる組み合わせ⑴、積が5になる組み合わせ⑵を考えます。
⑴1×2、⑵1×5になるのでたすき掛けすると
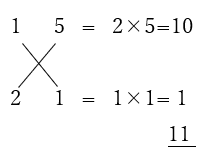
の組み合わせを見つけることができます。
この組み合わせを参考に因数分解すると
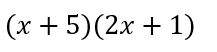
となります。
たすきがけの組み合わせを見つけるのが少し難しいかもしれません。
組み合わせは何回も計算することで慣れていくと思います！！
もう一問見ていきましょう。
積が6：1×6、2×3
積が-6：-1×6、1×-6、-2×3、2×-3
この組み合わせでたすき掛けしていきましょう。
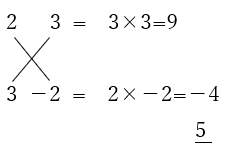
となるので答えは
となります。
組み合わせが見つけられましたか？
色々な因数分解
上で挙げた公式以外にも因数分解する方法があるので覚えておきましょう。
共通因数でくくる因数分解
係数が大きくなった場合、やみくもにたすき掛けするのではなくまずは共通因数を見つけましょう。
【例】
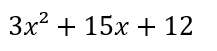
3が共通因数なので
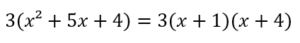
3乗の公式
次は3乗を含む式の因数分解について考えていきましょう。
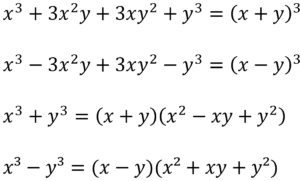
この公式が使えることを見抜けるのかがポイントです。
【例】
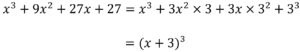
置き換えが必要な因数分解
式の中に同じ多項式が複数存在する場合置き換えを利用して因数分解を解くこともあります。
3x-1の部分をAと置き換えると
置き換えの部分をもとの式に戻すと
が答えになります。
因数分解ではここまで学んできた知識をどこで利用するかがポイントになってきます。
公式を頭に入れたうえで場面ごとに使える公式を選択できるようにしていきましょう。
まとめ
今回は因数分解について詳しく紹介してきました。
特にたすき掛けは練習が必要になってくるので繰り返し問題を解いていきましょう。
先ほど述べたように2次方程式、3次方程式を解くうえで因数分解は重要になってくるので公式も全部暗記するようにしましょう。
