2次方程式の解き方～因数分解・平方完成・解の公式～

こんにちは！オンライン家庭教師WAMです(^^)/

 

中学生になると、「1次方程式」「連立方程式」「2次方程式」と複数の方程式を習いますね。

今回はその中から、中学3年生で習う「2次方程式」についてお話したいと思います。

 

2次方程式とは

方程式について

2次方程式を話す前に、中学1年と2年で習う方程式について、少しおさらいをしましょう。

1年生で習う「方程式」は、正確には「1元1次方程式」と言います。

 

〈〇元〉は文字の数で、〈〇次〉は文字が何乗されているかを表します。

 

例えば、〈5x+1＝0〉であれば、文字はｘのみ、乗数は1なので「1元1次方程式」、

〈3x²+5＝0〉であれば、文字はｘのみ、乗数は2なので「1元2次方程式」となります。

 

2年生で習う「連立方程式」に関しては、xとyの2種類を使った方程式ですので「2元1次方程式」と呼ばれます。３つめの文字を使い、３つの式を連立させた「3元1次方程式」などもありますが、解き方の基本は同じです。

 

2次方程式とは

では、中学3年生で習う2次方程式は、どのようなものでしょうか？

一般式として、次のようなものが挙げられます。

 

 

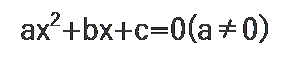
解きたい文字は1種類ですので、正確には「1元2次方程式」という呼び方が正しい呼び方になりますが、中学生までで2次方程式と言えば、「1元」の方程式ですので、名称からカットされる事が基本になります。

また、断り書きのように(a≠0)と書かれていますが・・・当然、a=0であれば1次方程式になりますので、このような断り書きがあります。「係数は自由だけど、が0だと成り立たないからね！」という事です。

 

そして、ここが重要！

これから先、もっと高次の方程式が出てくる事もありますが、例えば1次方程式は解が１つまで、2次方程式は解が２つまで・・・〇次方程式は解が〇つまで（それ以下もありえる）と、何次であってもそのルールは決まっています。

 

2次方程式を解くのに必要な知識

複雑そうに見える2次方程式ですが、主に3種類の解き方を駆使して、の値を求めていきます。その3種類のうち、2種類が同じく中学3年生で習う「因数分解」と「平方根」の知識を使った解き方です。

 

因数分解を使った解き方

因数分解とは

中学3年生になって、一番最初に習う数学の項目は「展開」というものです。

式が簡単な形になっていて、それを１つ１つの項にして、共通項の式同士はまとめるというものでした。

 

因数分解はその逆で、手順としては

１：共通因数でくくる（分配法則の逆）

２：公式を利用できるものは、さらに簡単な形にまとめる（さらなる分配法則の逆）

となります。

 

例として、以下の数式をを因数分解してみましょう。

 

 

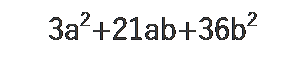
まず、いずれも３の倍数ですので全体を３でくくります。

 

 

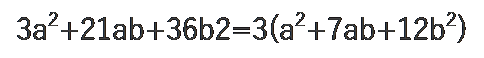
次に、足して7、かけて12になる数字の組み合わせを考えると、3と4があります。

 

 

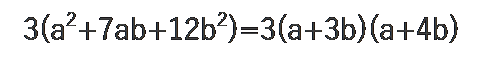
と、因数分解する事ができます。

 

実際に解いてみる

では、実際に因数分解を利用して、2次方程式を解いてみましょう。

 

 

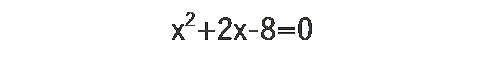
この式を因数分解すると

 

 

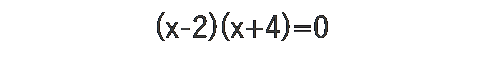
と、なります。

右辺を0にするためには、左辺の(x-2)か(x+4)を0にすれば、成り立ちます。

ですので、x-2=0と、x+4=0の両方を考えれば良い事になります。

ここまで来れば簡単ですね？

x=2とx=-4が正解となります。

 

2次方程式の解き方について
オンライン家庭教師WAMの体験授業で質問してみる

 

平方根を使った解き方

平方根とは

普段、何気なく使っている単位として、「㎠」「㎡」が挙げられます。

日本語で言うと、それぞれの単位に「平方」という言葉が使われていて、単位のほうには２乗を表す数字がつけられています。

平方根にも、同じ「平方」という言葉が使われていますよね。

これは「２乗したもの」という意味があります。

 

では「根」とは何でしょうか？

こちらは英語で言うとroot（根）という意味があります。

それらを合わせた「平方根」とは「与えられた数が2乗した数だとすると、その元となった数は何なのか？」という意味があります。

 

例えば「４」という数字ですが、これは２を2乗すれば出てくる数ですよね？

でも、-2を2乗しても、答えは４になります。

したがって、４の平方根は±2となります。

 

では問題ですが、２の平方根はと聞かれると、どうでしょうか？

実際に表せない数となるので、この場合は±√2（ルート２）と答えます。「2乗すると２になりますよ」という記号が、ルートという記号です。

 

平方完成

ではその知識を利用して、2次方程式を解いていきましょう。

 

 

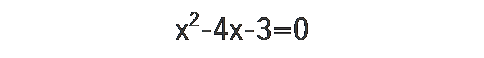
因数分解できそうで、できない形です。この場合は、無理やりの形を作ります。

 

 

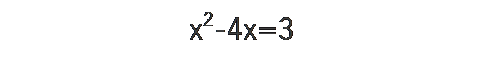
一旦、整数部分は右辺に移項します。

そして、左辺が一次式の2乗の形にできるようにを両辺に4を加えます。

 

 

左辺を平方完成にすると

 

 

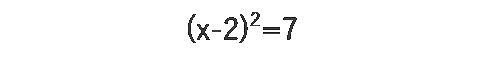
となり、両辺とも2乗の形を解くと

 

 

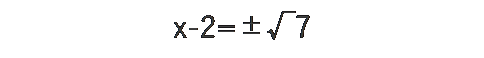
となります。-2を右辺に移項すると、x=2±√7という答えが導かれました。

 

解の公式を使った解き方

解の公式とは

今までは、既に習った数学の考え方での値を出してきました。

しかし・・・それが公式に当てはめると、一発で解けてしまうという魔法のような公式が存在します。

その名も「2次方程式の解の公式」という、名前だけ見ても「あ、これで解けちゃうんだ」と解る公式です。

上記の時、xを満たす数は、次のように表せます。

 

 

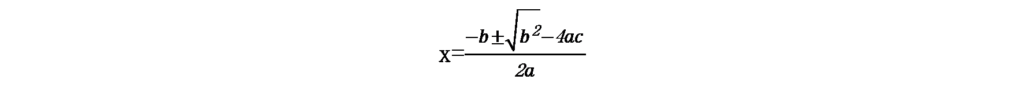
係数さえ解れば、ｘが求められるという公式です！

 

実際に解いてみる

この記事の、因数分解の時に出てきた式や平方完成で解いた式に「2次方程式の解の公式」あてはめてみましょう。

 

 

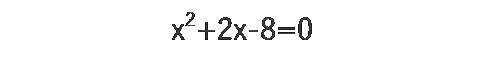
a=1、b=2、c=-8なので

 

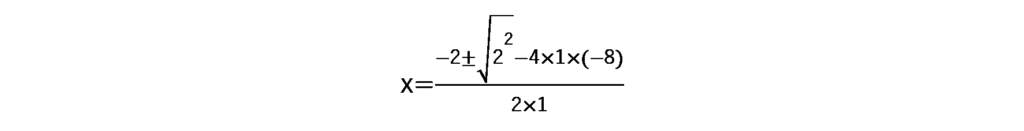
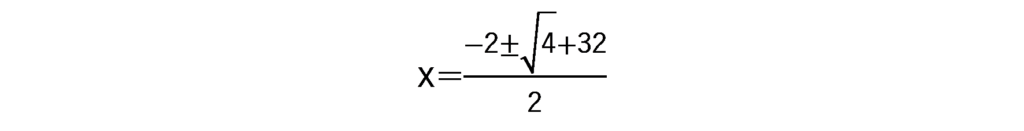
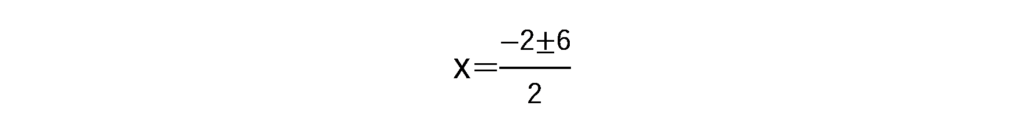
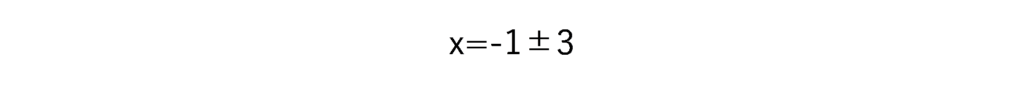
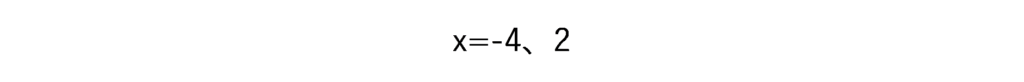
となり、正解になります。

 

 

では次に、平方完成に使った式です。

 

 

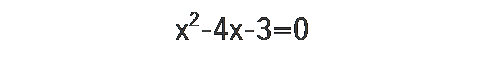
a=1、b=-4、c=-3なので

 

 

 

 

 

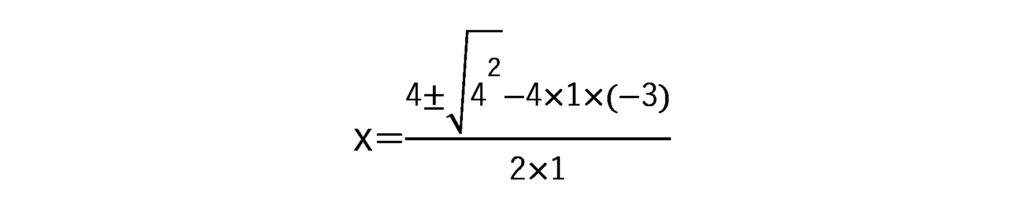
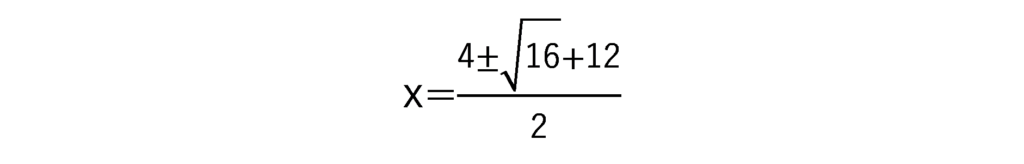
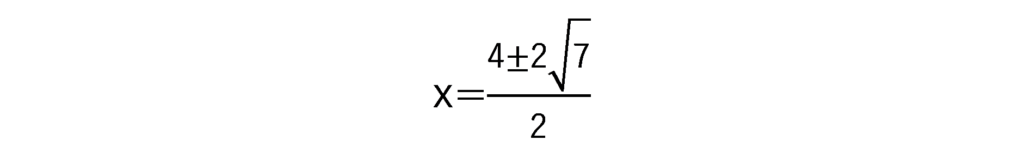
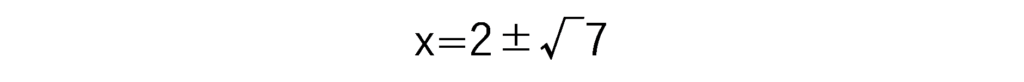
となり、やはり正解になります。

 

中学生では、ルートの中が負にならない限り、この公式は利用できます。

負になる場合は・・・高校以降のお楽しみとして、取っておいてください。

逆に言うと、ルートの中が負になるような問題は、中学生の間は出ませんので、安心して下さい。

 

 

公式を導き出す

ではなぜ、このような公式が成立するのか、実際に導いてみましょう。

注目する点は、a≠0という点と、平方完成にあります。

 

両辺をaで割ると　→aは0でないので、割る事ができる。

 

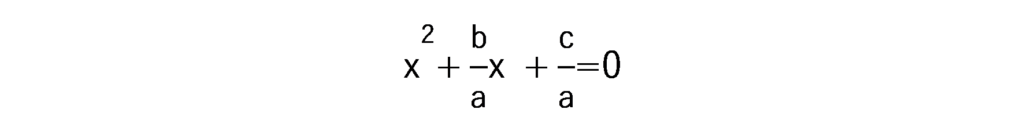
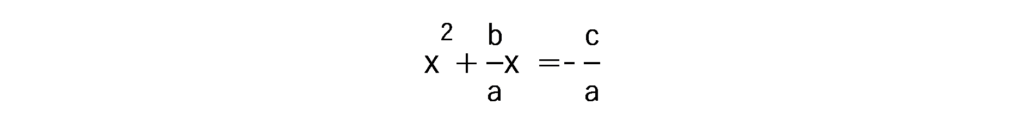
となり、左辺を平方完成させるため、両辺にを加えると

 

 

 

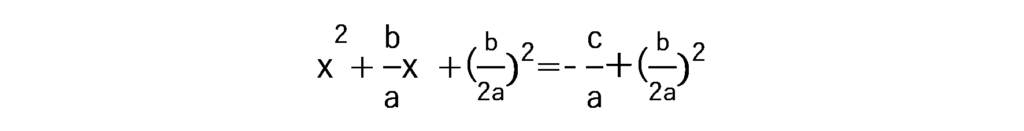
平方完成をさせ、右辺の分母をに統一する。

 

 

 

 

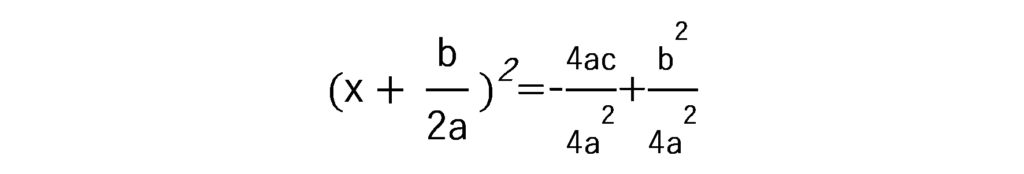
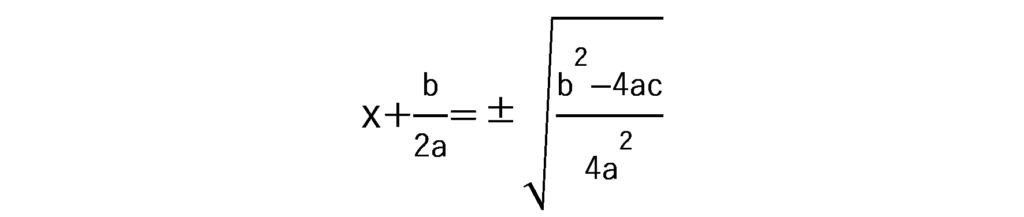
4a^2の平方根は、±2aなので

 

 

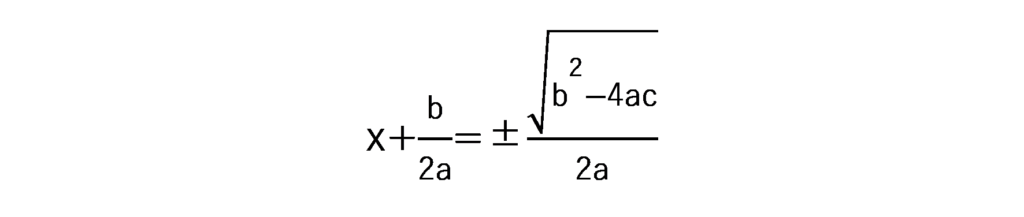
を右辺に移項すると

 

 

 

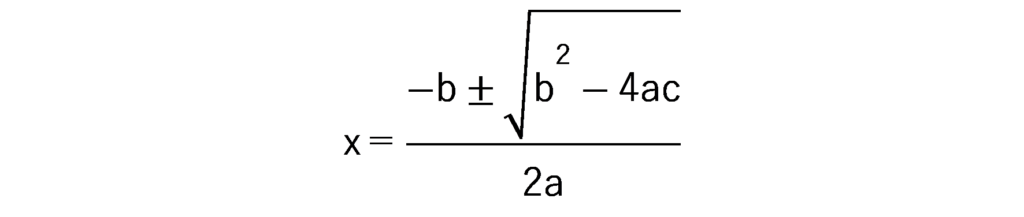
となり、それぞれの係数だけで、を導き出す事ができます。

 

 

 

まとめ～解き方の工夫～

２次方程式ともなると様々な解き方ができますが、少し乱暴な事を言ってしまうと、解の公式を使えば必ず解けます。しかし、係数をそれぞれ当てはめていく作業は意外と難しいんです。

そこで解く順番としては、

１：因数分解ができるか？

２：平方完成が簡単にできそうか？

３：１と２に該当しなければ、最終手段に解の公式を使う

が良いかと思います。

参考にしてみてくださいね。