「フーリエ変換」「デルタ関数」聞いたことありますか？

こんにちは！オンライン家庭教師WAMです(^^)/

「美味しいスイカは叩いた時の音で見分ける」という話を聞いたことはないでしょうか。

 

 

スイカを叩いた音と味の関係は分かりませんが、そもそも、このスイカを叩いて音を調べるという行為にはどのような意味があるのでしょうか。

 

この記事では、「物を叩いて出る音を調べる」ということの科学的な意味について、フーリエ変換やデルタ関数というものを使って説明します。

 

フーリエ変換とデルタ関数

フーリエ変換やデルタ関数と聞くと、とてもカッコいい名前だと思う反面、とても難しそうな印象を持たれるのではないでしょうか。

まずはこの２つの事柄について、数式は一切使わず説明をしていきます。

説明を分かりやすくするため、ところどころ曖昧な部分や簡略化している部分があります。

あらかじめご了承ください。

また、この話を読んでもお店に置いてあるスイカは叩かないでくださいね！

 

フーリエ変換と波の振動について

まずは、フーリエ変換について説明していきます。

 

フーリエ変換の「フーリエ」は、Joseph Fourier(ジョゼフ フーリエ)さんという、フランスの数物理学者の名前から来ています。フーリエさんが発見した「フーリエ展開」というものが基になって、「フーリエ変換」が生まれました。

 

このフーリエ変換の使いみちの一つに、「音の波のデータをフーリエ変換すると、その音声の中に高い音や低い音がどのくらい含まれているのかが分かる」というものがあります。

 

 

例えば、人間が声を出す時は喉にある声帯と呼ばれる部分を振動させます。

声帯の振動が空気を震わせて波（音波）ができ、音波が空気を通して鼓膜に届くことで音が伝わります。

 

 

音の高さというのは、その音の波の1秒あたりの振動回数で決まります。

振動の回数が多ければ高い音になりますし、逆に振動の回数が少なければ低い音になります。

 

下の画像をご覧ください。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

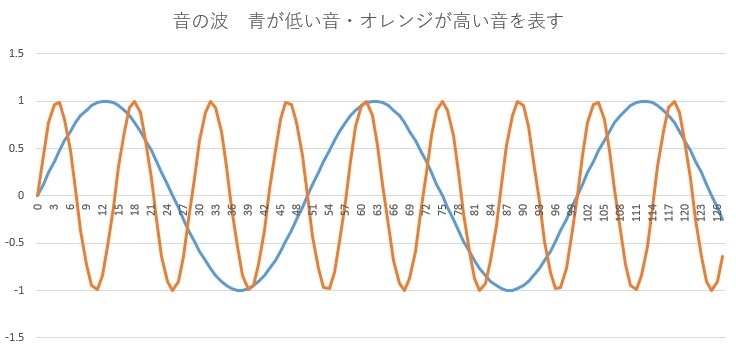
青とオレンジの線で描かれた２つの波があります。

 

青の波よりオレンジの波の方が、たくさん山と谷があります。

この波を音の波だと思うと、オレンジの波の方が青の波より振動の数が多いため、オレンジの波の方が高い音だということになります。

 

フーリエ変換に話を戻しますが、波に対してフーリエ変換を使うと、その波の振動の様子が分かります。

これから実際に、フーリエ変換で波の振動の回数を調べてみましょう。

 

フーリエ変換で波の振動の様子を見る

波をフーリエ変換すると、その波の振動の回数が分かります。

 

実際に先程の青い波をフーリエ変換し、振動の様子を見てみましょう。

 

 

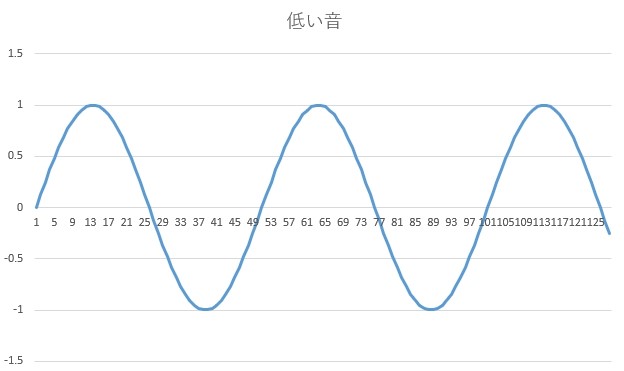
なお、これから「フーリエ変換したグラフ」というものをいくつかお見せしますが、本当はフーリエ変換した後にいくつか手を加え、分かりやすくしたグラフをお見せしています。

 

 

さて、下の画像が青い波をフーリエ変換したグラフです。

 

 

 

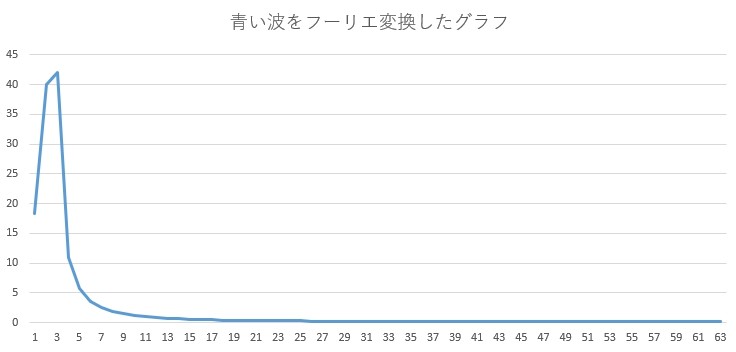
フーリエ変換後のグラフを見るときは、出てきた山の「横軸の位置」が重要になります。

 

上のグラフにある山は、横軸が「2」から「3」の真ん中ぐらい、約「2.5」の位置にあります。

この「2.5」という数字は、波の山と谷を1セットとして数えた時のセット数を表しています。

 

先程のグラフをもう一度確認してみましょう。

 

 

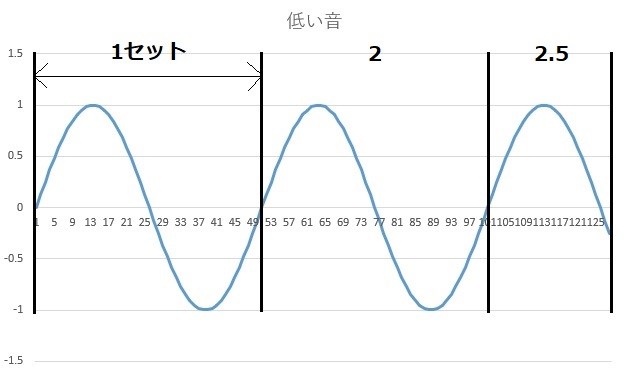
青い波の山と谷を1セットとして数えると、全部で約2.5セットあるのが分かります。

最後の部分は谷がなく山だけになっているので1セットの半分、0.5セットと数えました。

 

先程のフーリエ変換したグラフでは2.5の辺りに山ができていました。

青い波のグラフで数えたセット数と一致しています。

 

 

次はオレンジのグラフをフーリエ変換します。

 

 

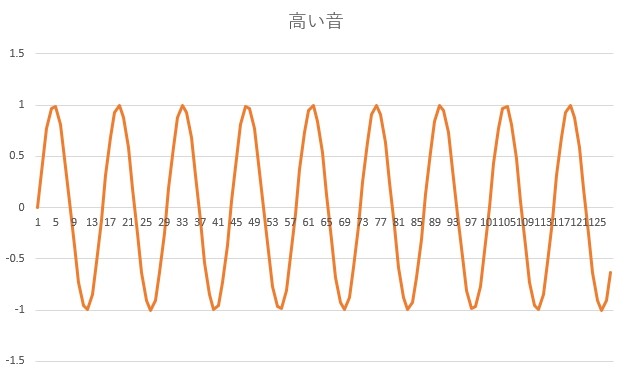
すると次のようなグラフになりました。

 

 

 

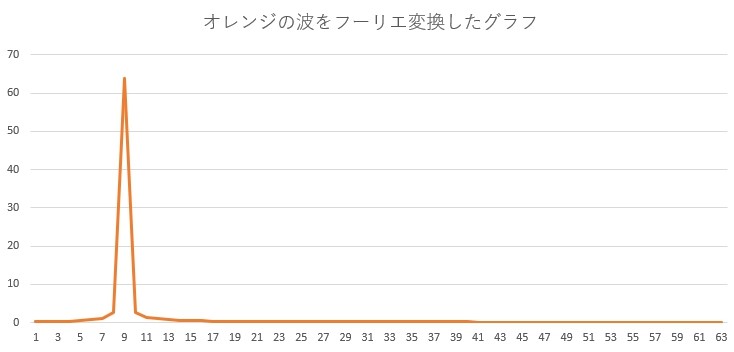
横軸が9のところに山ができています。

 

オレンジのグラフを見ながら山と谷のセット数を数えてみると、最後の方は少し見切れていますが、約9セットあるのが分かります。

 

 

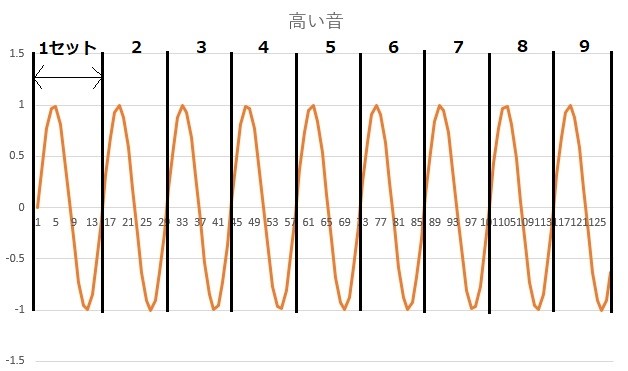
オレンジのグラフでも、フーリエ変換の結果とグラフから読み取ったセット数が一致しました。

このように、フーリエ変換を行うと、山と谷をセットにしたものの数（つまり振動の回数）が分かります。

 

複雑な波をフーリエ変換する

しかし、これだけだと、「山と谷のセット数を知りたいなら、フーリエ変換なんて使わなくてもグラフを見ながらセット数を数えれば良いじゃないか」という声が聞こえてきそうです。

 

フーリエ変換が力を発揮するのはこれからです。

今度は下の画像の複雑な波についてセット数を数えてみましょう。

 

 

 

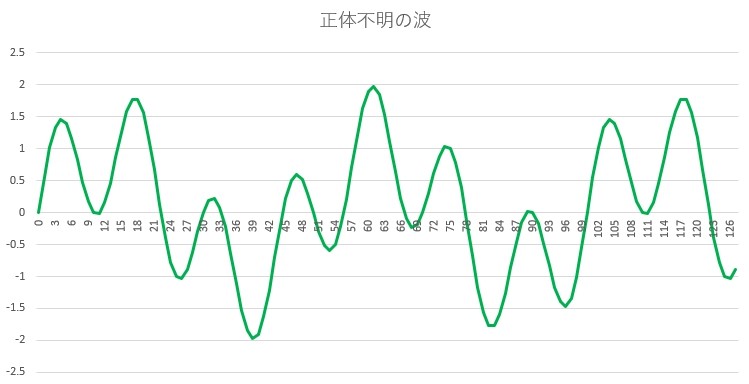
セット数を数えたくても、どこまでを1セットとすれば良いのか分かりません。

 

では、このグラフをフーリエ変換してみましょう。

するとこのようなグラフが出てきました。

 

 

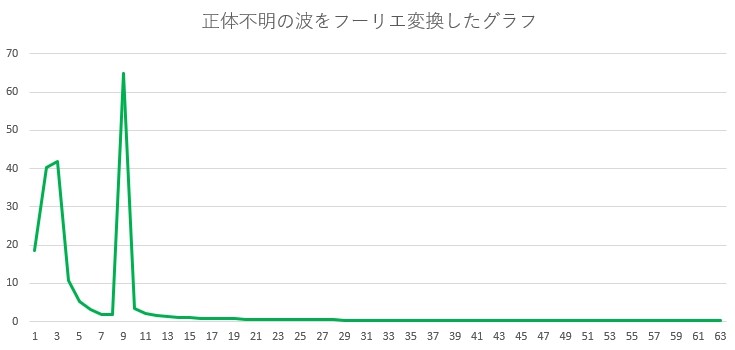
横軸が「2.5」と「9」の付近に、山ができています。

 

皆さんお気付きでしょうか。

この「2.5」は青い波のときと同じ波の数で、「9」はオレンジの波のときと同じ波の数です。

何を隠そう、先ほどの複雑な緑の波は、青の波とオレンジの波を足し合わせて作ったものだったのです。

 

 

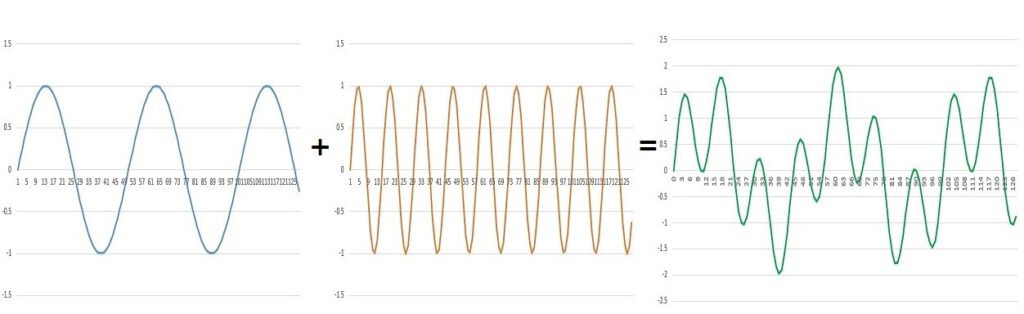
このように、複雑な波というのは、実はいくつかの単純な波を組み合わせて作られていることがあります。

フーリエ変換を行うと、複雑な波の中に隠された単純な波を分離して探し出すことができるのです。

 

 

デルタ関数について

これまでフーリエ変換について書いてきました。

これからデルタ関数についても書いていきますが、こちらは短く簡単に説明します。

 

デルタ関数とは、ポール・ディラック（Paul Dirac）という物理学者が使い始めた関数です。

中学校で習う一次関数のような、いわゆる“普通“の関数とは違うので、「超関数」と呼ばれています。

 

デルタ関数をグラフにすると下の図のようになります。

 

 

 

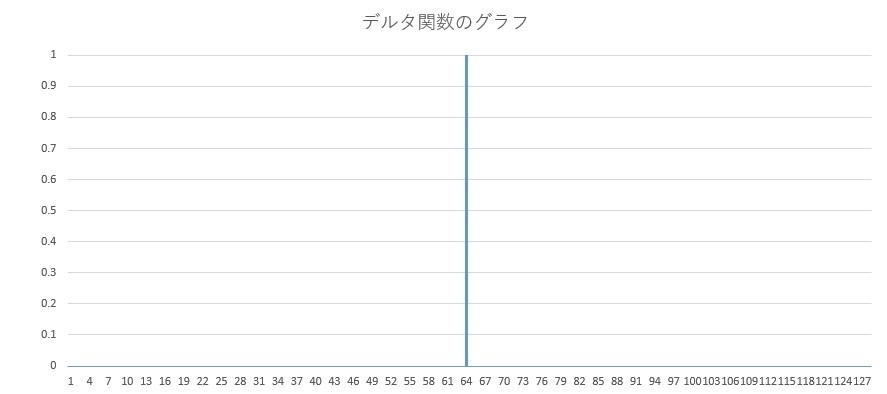
真ん中辺りに一本の高い針（値は無限大）が立っていますが、それ以外のところは全て値がゼロになっています。

とても変わった関数です。

 

このデルタ関数は、一体どんな用途に使われるのでしょうか。

 

これからデルタ関数の使いみちについて触れつつ、フーリエ変換を使いながら、ページの冒頭で述べた「スイカを叩いて音を調べることの意味」について書いていきます。

 

デルタ関数とスイカを叩く音

スイカ（スイカ以外の物でも良いのですが）を叩いたときの音は、まさしくデルタ関数で表すことができます。

 

スイカを叩くと一瞬だけ「ポン」と音が鳴ります。

その一瞬の音を表しているのがデルタ関数の針の部分です。

 

 

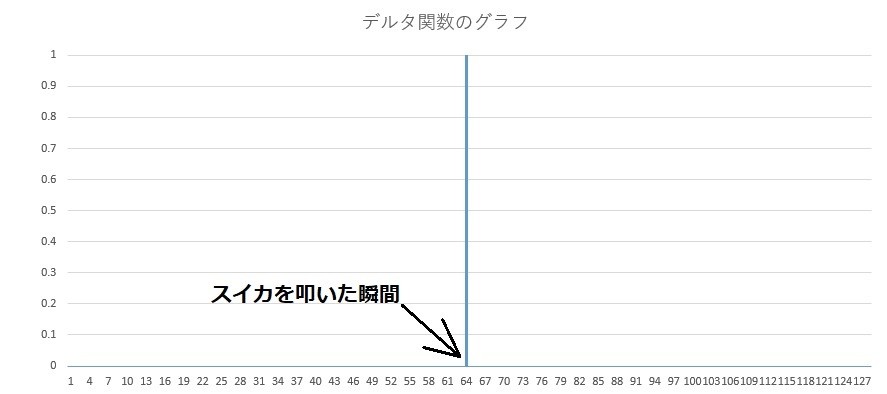
デルタ関数は、このように一瞬の出来事を表すために使うことができます。

 

 

ところで、この一瞬の音を表しているデルタ関数をフーリエ変換すると、どのようなグラフになると思いますか？

つまり、一瞬の音にはどのような高さの音が含まれているのでしょうか。

 

すぐに答えは出しません。

他の関数で少し実験してみましょう。

 

下の図の左側にある、幅の広い山をフーリエ変換すると右のグラフになります。

 

 

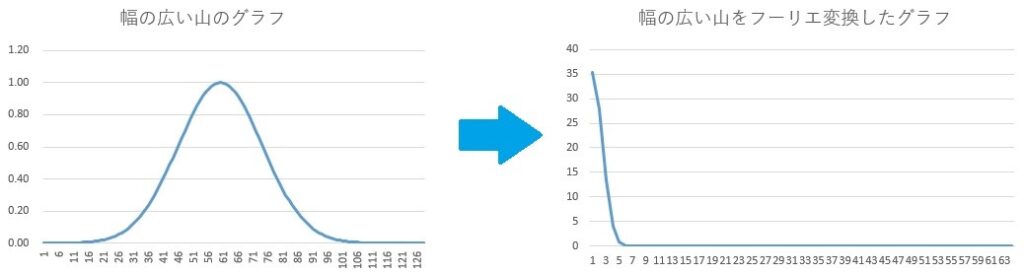
半分に見切れていますが、幅の狭い山になりました。

 

 

今度は幅の狭い山をフーリエ変換してみます。

 

 

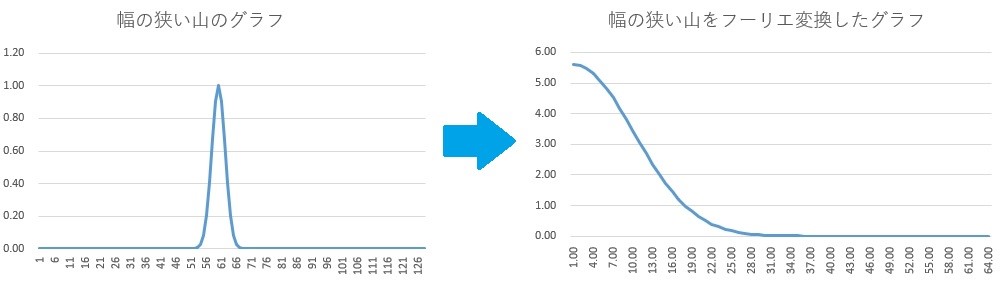
さっきのフーリエ変換のグラフよりも幅の広い山が見えています。

 

 

では、さらに山の幅を狭くしていき、一本の針のような山（つまりデルタ関数）をフーリエ変換するとどうなるのでしょうか。

 

予想してみてください。

 

答えは下のグラフになります。

 

 

 

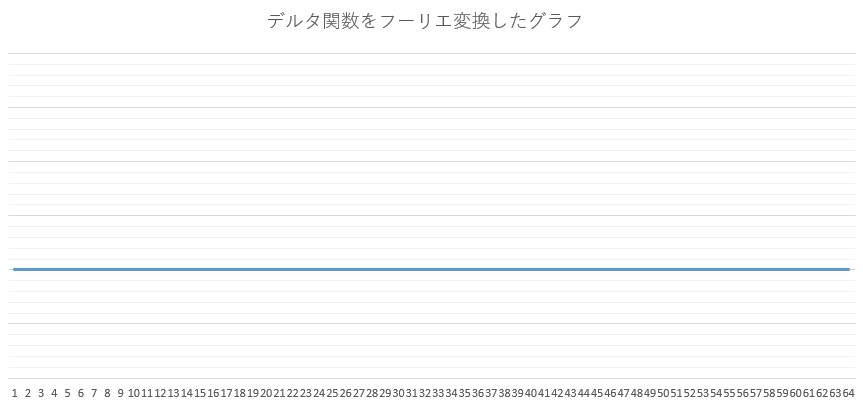
どの点も同じ値の平らなグラフが出てきました。

デルタ関数をフーリエ変換すると、全ての点が同じ値を持つ、平らなグラフになるようです。

 

さて、フーリエ変換の意味を思い出してみましょう。

音のデータをフーリエ変換すると、その音に高い音や低い音がどれだけ含まれているのかが分かるのでした。

 

今回の結果から、「物を叩くような一瞬の音には、高い音から低い音まで、いろいろな高さの音が含まれている」ということが分かります。

 

 

物を叩くという行為は、「物にいろいろな高さの音をぶつける」という意味を持っています。

 

物質によって叩いたときの音が違うのは皆さんご存知のとおりです。

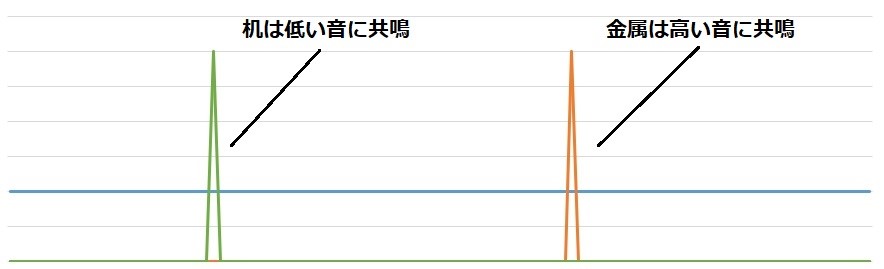
金属を叩くと高い音がし、机を叩くと低く鈍い音がします。

 

叩くというのは全ての高さの音をぶつけるという行為だと書きましたが、その色々な高さの音に対し、音をぶつけた物質の種類や構造によって、共鳴する音の高さが違います。

金属を叩くと、金属は叩いた音の中にある高い音に共鳴し、机は低い音に共鳴します。

そのため金属を叩くと高い音が聞こえ、机を叩くと低い音が聞こえるのです。

 

ところで、物質は内部の構造によっても共鳴する音の高さが違います。

 

 

例えば金属は、中空（中が空いていること）になっているか詰まっているかで叩いたときの音が変わるため、金属を叩くことで中がどうなっているかを調べることができます。

スイカを叩くのも同様で、スイカの内部の状態によって増幅される音の高さが決まるため、スイカを叩くことで中身の検査をすることができるのです。

 

 

まとめ

いかがでしたか？

物を叩くという行為には、全ての高さの音をぶつけるという意味があります。

そして、どの高さの音に物質が共鳴するかを見ることで、対象の種類や中身を検査することができます。

数学や理科を勉強していくと、このような物事に隠された意味をより深く知ることができるようになります！

いろんなことに興味を持って、楽しく学習できると良いですね。