基本中の基本?!一次方程式の解き方

こんにちは!オンライン家庭教師WAMです(^^)/
本日は【基本中の基本?!一次方程式の解き方】についてお話します。
中学校に入ってまず勉強する一次方程式。
最初の概念を理解するのが一番難しいです。
そもそも一次方程式って何だろう…そんな疑問を今回の記事で解決していければと思います。
Contents
一次方程式の解き方
まずは一次方程式の解き方について解説していきたいと思います。
一次方程式とは一次式、つまり一番大きい次数が1である式のことです。
簡単に言うとx²とかx³などの次数の高いものを含まず、x、yなどの単純な文字と数字のみの方程式のことです。
では例題を見ながら解いていきましょう。

この方程式を解いていきましょう。
基本的な方程式の解き方は
①文字は左辺、数は右辺に移項
②xの係数を両辺で割る
ここで、まず移項とは?ということについて説明します。
移項とは簡単に言うと足し算、引き算の式において符号を変えて式の右辺→左辺もしくは左辺→右辺に移動させることです。
なんで符号をかえるの??
そんな疑問を持つ人もいると思います。
例題の式でみていきましょう。

左側に文字を持っていきたいので右辺の文字の部分つまり8xが邪魔ですね。
等式においては両辺に同じものを足したり引いたりしても等式の関係は変わらないので両辺から8xを引いていきます。
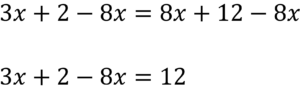
ここでもとの式を比較すると

![]()
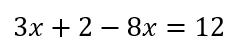
結果的に右辺の8xの符号をマイナスに変えて左辺に移動しているのがわかると思います。
これが「移項」です。
同様に左辺の2も移項すると
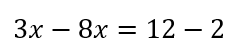
となり、これを計算すると
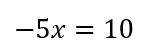
これで①の作業が完了です。
次は②xの係数を両辺で割る作業です。
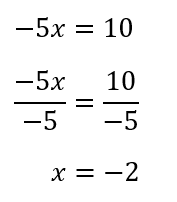
これが答えになります。
念のためx=-2をもとの式に代入すると等式が成り立つことがわかると思います。
基本はこの手順で一次方程式を解いていきます。
一次方程式で間違いやすいのは移項の時の符号ミス、xの係数で両辺を割ったときの符号ミスです。
符号には十分に注意しましょう!!
ではこれらのポイントを踏まえて何問か練習問題を解いていきましょう。
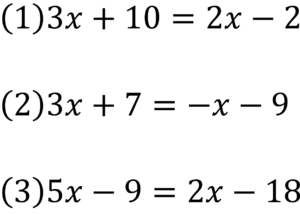
解けましたか?
答え合わせしていきましょう。
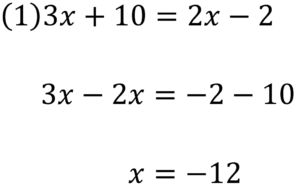

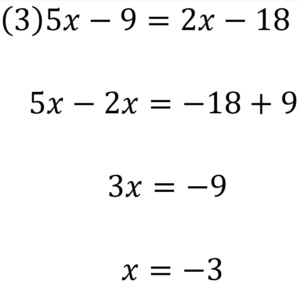
符号に気を付けて解けましたか?
この計算は基本になるのでしっかりマスターしておきましょう。

小数・分数を含む一次方程式の解き方
ここからは応用問題を解いていきましょう。
小数を含む方程式
小数を含む方程式は少し工夫が必要です。
例題を見て考えていきましょう。
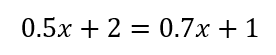
このまま計算していっても答えを導くことはできますが、少し工夫して解けば計算ミスを減らすことができます。
ポイントは「小数を含む式ではなく整数のみの式にすること」です!
例題の場合は、10を掛けると整数になりますね。
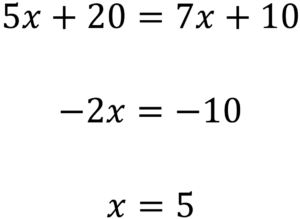
計算しやすくなりましたね。
では、もう一問見てみましょう。
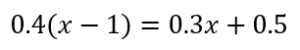
この場合も同様に解いてみましょう。
まずは両辺に10をかけて
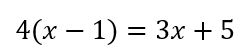
分配法則を用いて()を外すと
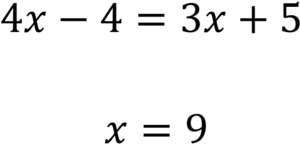
分数を含む方程式
分数を含む式も少し工夫が必要になってきます。
では例題を見ていきましょう。
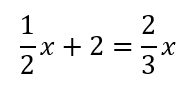
この場合も整数のみの式になるように変形していきます。
分母の「2」と「3」を消したいので最小公倍数である「6」を両辺にかけます。
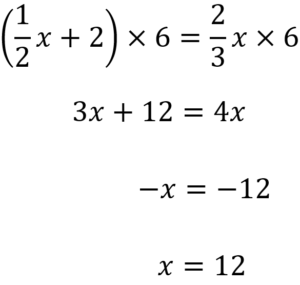
では以下のような場合はどのように解けばよいでしょうか。
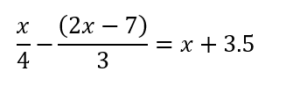
この場合は小数もしくは分数にそろえて解いていきましょう。
今回は分数に合わせて解いてみましょう。
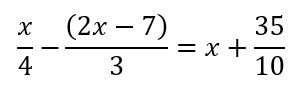
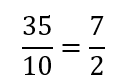 なので
なので
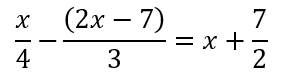
「4」と「3」と「2」の最小公倍数は「12」なので両辺に「12」をかけると
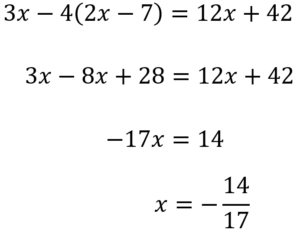
では例題を見ていきましょう。
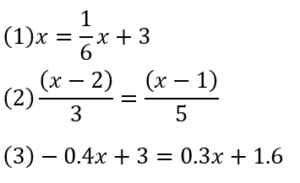
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
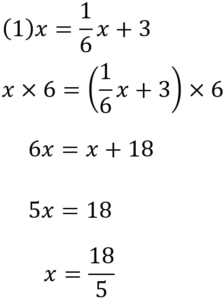
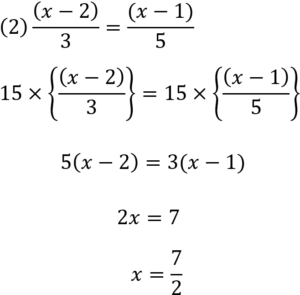
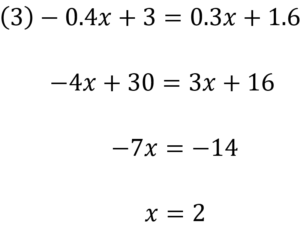
文章問題にチャレンジ!
代金の問題
文章問題で頻出の代金の問題について考えていきましょう。
オレンジジュースを3本と300円のケーキを2個買って代金780円になりました。
オレンジジュース1本の値段を求めなさい。
オレンジジュースの値段を1本x円とするとオレンジジュース3本分の値段は
3×x=3x(円)になります。
ケーキ2個の値段は300×2=600(円)
よって
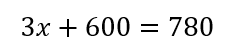
という式を作ることができます。
この式を解けば
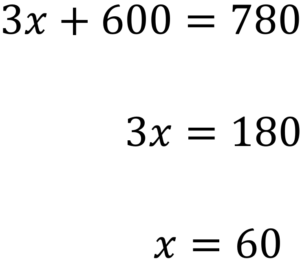
よってオレンジジュース1本の値段は60円になります。
定価・原価・利益の問題
そもそもの言葉の意味は以下のようになります。
定価…原価にいくらかの利益をみこんでつけた値段
原価…小売店が業者から商品を買い入れた値段。仕入れ値とも言います。
利益…原価と売値の差
この3つの関係は
定価=原価+利益
となります。
実際に問題を見ていきましょう。
Aさんは洋服を仕入れて、原価2割(20%)の利益を見込んで定価をつけましたが、定価から400円の値引きをして売ったので、利益は原価の1割2分(12%)になりました。
この商品の原価はいくらですか。
洋服の値段をx円とおいてみましょう。
定価はx+0.2x(見込んだ利益) 円と表すことができます。
また、実際の利益は0.12x 円と表せます。
売値=原価+利益と表すことができるので、

よって答えは5000円になります。
食塩水の問題
8%の食塩水が500gあります。この食塩水に水を加えて5%の食塩水を作る時、加える水を何gにすればよいかを求めなさい。
加える水の量をxgとして考えていきましょう。
まず初めの食塩水中の食塩の量は500(g)×8/100=40g
この食塩水に水を加えても食塩の量は変化しないので
(500+x) ×0.05 =40
全体の食塩水 濃度 食塩の量
この方程式を計算すると
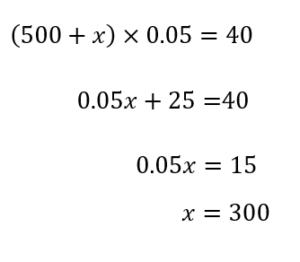
答えは300gになります。
一次方程式の文章問題では文章の内容を理解し、式を立てることが一番のポイントです。
分かりにくい場合は図を利用するなどして状況をしっかり理解するようにしましょう。
まとめ
今回は一次方程式について解説してきましたが、解き方のポイントは理解できましたか?
数学の基本中の基本になるので、ここでつまずかないようにしっかり復習しておきましょう。
また、移項の符号ミスはよくある間違いなので十分に注意しましょう。










 0120-333-876
0120-333-876






