二次方程式   

こんにちは！オンライン家庭教師WAMです(^^)

一次方程式の解き方はもう完璧！という方！
方程式は一次方程式だけではありません。二次関数を含む二次方程式も存在します。 

二次方程式の解き方にはいくつかポイントがあるので、今回は気を付けるべきポイントを紹介していきます。 

 

 

二次方程式の解き方 

まずは二次方程式の解き方について解説していきましょう。 

いくつかに場合分けできるので、どの方法が適切か見極めて解いていく必要があります。 

方法としては主に3つ存在します。 

 

①平方根を利用する 

②因数分解を利用する 

③解の公式を利用する 

 

まずはこの3つを使いこなせるようにしていきましょう。 

 

①平方根を利用する 

この方法は利用できる場面がかなり限られてきます。 

平方根で答えを出せる場合は以下のような形になります。 

 

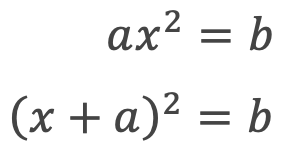
解き方はシンプルです。 

通常の平方根を求めるように根号を付けるだけです。例題を見ていきましょう。 

 

 

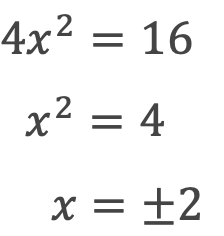
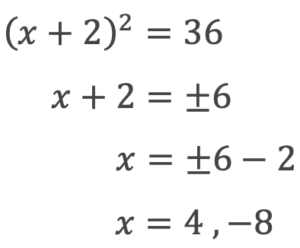
この方法が最も簡単に解くことができるので、この形に当てはまったらラッキーですね。 

 

②因数分解を利用する 

この場合はまず共通因数でくくることができるのかを見極めましょう。 

左辺に移行すると 

 

共通因数(x)でくくると 

このように2つの解を求めることができます。 

 

共通因数でくくれないとき、他の因数分解の公式を思い出してみましょう。 

因数分解の公式をひらめくと二次方程式を解くことができるのです。 

因数分解すると 

 

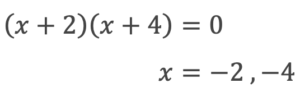
因数分解を使うと、全体的に計算量が減って計算ミスを減らすことができます。

因数分解ができるのか常に意識しながら解くようにしましょう。 

 

③解の公式を利用する 

この解き方は基本的にどんな二次方程式でも解くことができます。 

なら、この解き方で全部解けばいいのでは？？
唯一の欠点は計算が若干複雑であるという点です。 

そのため、できるだけ他の解き方を検討してみて最後の手段といったイメージですね。 

 

解の公式はとりあえず声に出して暗記しましょう。 

 

 

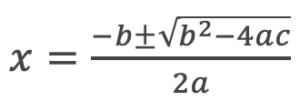
この式は因数分解できませんね。 

そこで解の公式の出番です。 

  

             

 

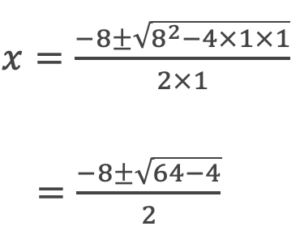
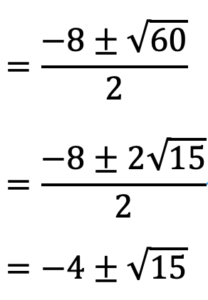
これが答えになります。 

なんといっても計算ミスには要注意です。 

 

どの解き方を使うか見極めましょう。

 

二次方程式の計算をより早く正確に行うには、どの方法を使うかを見極めることが重要になってきます。 

以下の順序を追って考えてみましょう。 

①平方根を使えるか 

②共通因数でくくれるか 

③因数分解できるか 

(④たすき掛けができるか) 

⑤解の公式を使う 

 

①から順に検討していって「No」であったら次のステップに進むというように考えていきましょう。 

計算が簡単なものから検討していって、無理であったら解の公式を使うというイメージですね。たすき掛けについては今回は触れないので気になった人は参考書などで確認してみてください。 

 

では例題を見ていきましょう。 

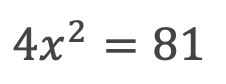
まずは①平方根を使えるかを考えるとこの式では平方根の解き方が適用できますね。 

 

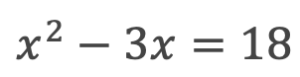
この場合はまず、①平方根は使えなさそうですね。 

次に、②共通因数でくくるのも難しそうですね。 

では、③因数分解を考えてみましょう。 

このままでは因数分解の公式を当てはめられないので左辺に移行していきます。 

 

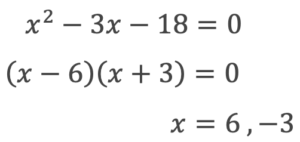
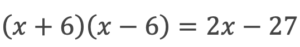
まずは式を簡単にして左辺に集めていきます。 

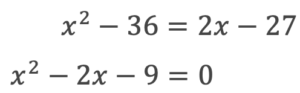
この場合は①平方根が使えない②共通因数でくくれない③因数分解の公式が使えない 

そこで⑤の解の公式を用います。 

 

 

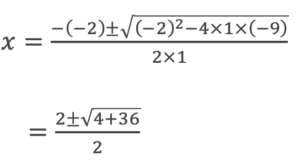
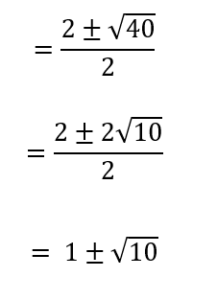
このように、順を追って考えていくことで計算ミスを防ぐことができます。 

この見極めは計算演習を重ねていくことで身につけていきましょう。 

 

 

文章問題を解いてみよう 

最後に二次方程式を利用した文章問題を解いていきましょう。 

 

自然数に関する問題 

連続する3つの自然数がある。大きいほうの2つの数の積が3つの数の和に等しい時この3つの自然数を求めなさい。 

 

ここでポイントになるのは「連続する3つの自然数」です。連続するので 

n,n+1,n+2 

と表すか 

n-1,n,n+1 

と表します。 

今回はn,n+1,n+2で表してみましょう。 

 

大きいほうの2つの積⇒(n+1)(n+2) 

3つの数の和⇒n+n+1+n+2=3n+3 

 

大きいほうの2つの積が3つの数の和と等しくなるので 

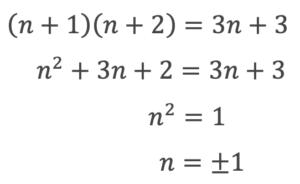
nは自然数なので、n=1となり、答えは１、２，３です。 

 

このように2次方程式を用いて整数を求めていきましょう。最後に自然数であるという条件を見逃さないようにしましょう。 

 

図形面積の問題 

長さ28cmのひもで長方形を作り、面積が45㎝²になるようにしたい。このときの長方形の縦と横の長さを求めなさい。 

 

ここでポイントになるのは 

長さ28㎝のひも＝２×(縦＋横) 

であるということです。 

長方形には縦、横は2辺ずつ存在するのでひもの長さは縦2辺、横2辺が含まれていることに注意しましょう。 

縦の長さをｘ(㎝)とすると 

28=2×(x＋横) 

であるので 

14＝ｘ＋横 

横の長さは14‐x(㎝)と表すことができます。 

 

さらに面積が45㎝²であるので 

 

どちらの条件でもひもの長さ28㎝を超えないので答えは5㎝、9㎝になります。 

 

花壇の道幅を求める問題 

縦15m、横18ｍの長方形の形をした土地に同じ道幅の道路をつくって周りを花壇にしました。この時の花壇全体の面積が180m²になる時の道幅を求めなさい。 

 

道幅の問題では道を端に寄せて考えます。 

この問題では道幅をx(ｍ)とすると花壇の縦の長さは15-x(m),横の長さは18-x(m)になります。この花壇の面積が180m²になるので 

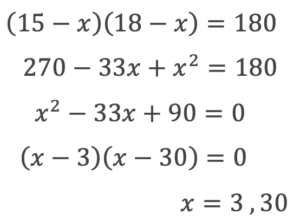
道幅は土地の縦、横の長さを超えてはいけないので道幅は３mが答えになります。 

道が増えても同じような考え方で考えていきましょう。 

 

動点問題 

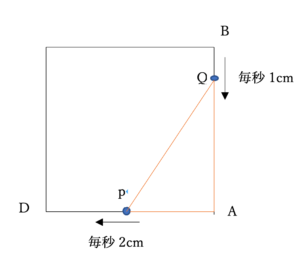
下の図のような一辺10㎝の正方形ABCDの辺上を動く点P、Qがある。

点Pは頂点Aを出発して毎秒2㎝の速さで点Dに向かって動いていく。一方で点Qは頂点Bを出発して毎秒1㎝の速さで点Aに向かって動いていく。

点P、Q、Aで作る三角形の面積が16㎝²になる時は何秒後かを求めなさい。 

ただし点Pが点Dに到達するまでの間とする。 

求める答えをx秒後とすると 

点Pは毎秒２㎝動くのでx秒後には2x(㎝)動く 

よってAP＝2x(㎝) 

次に点Qは毎秒1㎝動くのでx秒後にはx(㎝)動く 

よってBQ＝x(㎝)なのでAQ＝10－ⅹ(㎝) 

よって

 

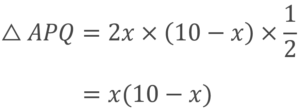
この面積が16㎝²なので 

 

 

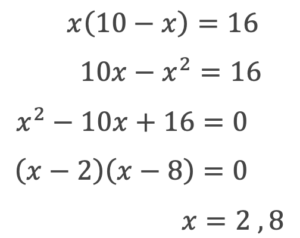
点Pが点Dに到達するのは10÷２＝5秒後なので答えは2秒後となります。 

 

この他にも二次方程式を利用した問題はたくさんあります。 

ポイントとなるのはどの変数をxと置くか、xの範囲に答えは入っているのかです。 

 

 

まとめ

今回は二次方程式について解説してきましたが理解できたでしょうか。 

きちんと手順通りに解いていけばきっと解けるようになるはずです。 

二次方程式の文章問題はテストでも頻出なので確実に身に着けていきましょう。