絶対値と不等式が分からない!問題の解き方はどうする?

こんにちは!オンライン家庭教師WAMです(^^)/
今回は【絶対値と不等式が分からない!問題の解き方はどうする?】についてお話します。
「絶対値」を初めて学習するのは、中学1年生の「正負の数」。
正負の数の計算は、中学校に入って最初に苦戦する単元です。
最初が肝心と言いますが、数学にも当てはまります!
今回述べていく「絶対値」も中学校から学び、高校・大学でも学習していきます。
人によっては仕事でも使うことがあるかもしれません。
そのため最初に学んだ時に、分かるまで勉強しておくことが大切ですね!
Contents
絶対値ってそもそもなんだろう?
では、そもそも「絶対値」とは何の値を示しているのでしょう。
いざ問われると答えづらくありませんか?
「なんとなくのイメージはできるけれど、はっきりと説明はできないかも…。」
「絶対の値…?」
たしかに、正しく説明しようとすると難しいですよね。
ではここで絶対値について確認していきましょう!
絶対値の定義
絶対値とは、『数直線上において、ある数字が原点0からどれだけの距離にあるのかを表している値』になります。
言葉だけだと、イメージしづらいですね。
では、分かりやすい例を使って説明していきます。

このような温度計を見たことはありませんか?
(なければ、天気ニュースの気温をイメージしてください。)
0より上の数字を示していれば、「+何℃」
0より下の数字を示していれば、「-何℃」
このように表されています。
例えば、「+10℃」「-10℃」の2つを確認してみましょう。
「+10度」→0℃を基準値として、それより10℃高い
「-10度」→0℃を基準値として、それより10℃低い
ということを指しているのです。
つまり、0℃を基準として同じ数字分だけ高いか低いかを示しているのです!
絶対値の記号
さて、絶対値のイメージは掴めたかと思います。
しかし、毎回温度計を取り出してくることは不可能だと思います。
(テストで温度計を持ち込むことはできないですしね!)
そのため、数式に出てくる絶対値を見てみましょう。
絶対値は「||」という記号を使って表されます。
具体例を出して実際に確認してみましょう。
「2」と「-2」の2つの数字を使います。
「2」の絶対値は|2|、「-2」の絶対値は|-2| と表します。
数字を棒で挟むだけなので、とっても簡単です!
記号のはずし方
では、絶対値を表す記号「||」を外してみましょう。
ただ、「||」で挟まれたものが数字だったり、文字だったりします!
2つのパターンに分けて、確認していきましょう。
数字のパターン
結論から述べると、
|5|→5
|+5|→5
|-5|→5
このようになります。
||の中身が負の数のときは、その数に「-1」をかけたものが絶対値になります。
||の中身が正の数でも負の数でも、符号をはずしたものがその数値の絶対値となるのです!
文字のパターン
文字の場合は、数字と違って少しややこしいです…。
(|X|や|X-5|のようなものがあります。)
ここは理解できるまで、じっくり読んでください!
文字の場合は、||の中が正の数のときと負の数のときの2パターンを考えないといけないのです。
|X|のとき
X>0(Xが正の数)のとき、|X|=X
X<0(Xが負の数)のとき、|X|=-X
|X-5|の場合
X-5>0(X-5が正の数)⇒X>5のとき、|X-5|=X-5
X-5<0(X-5が負の数)⇒X<5のとき、
|X-5|=-(X-5)=-X+5
このようになります。
数字の場合のときも述べましたが、
||の中身が負の数のときは、その数に「-1」をかけたものが絶対値です!!
絶対値の基本を確認しておこう!
ここまで、絶対値の基本の基本を見てきました。
では次に、実際に絶対値を使ってみましょう!
数直線のおさらい
数直線は、一つの直線に数を対応させて表した図です。
0(原点)が中央にあり、同じ幅ずつ左右に目盛がつけられています。
0から右に行くと、正の数を表し、左に行くと負の数を表しています。
絶対値を求めるうえでも、利用できるものの1つです。
そのため、この数直線は暗記していつでもイメージできるように、
そして、書けるようにしておきましょう!
絶対値を求めよう
では、数直線を使って絶対値を確認していきましょう。
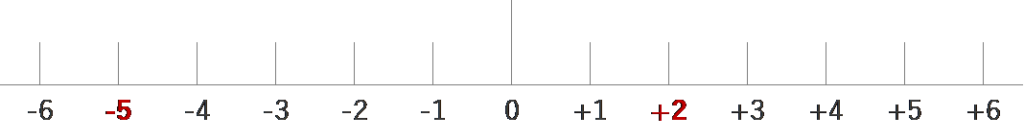
絶対値は、0からの距離を表した数値でしたね!
「+2」は0からの距離が2なので、「+2」の絶対値は2。
「-5」は0からの距離が5なので、「-5」の絶対値は5となります。
また、「0」の絶対値は0となりますので、注意してくださいね!
絶対値の大小
正負の数において、大小を比べるのに数直線や絶対値を使うと分かりやすいです!
例えば、「+4」と「+10」ではどちらが大きいでしょう?
絶対値として考えても求められますし、数直線で考えても求められますね!
これは小学生でも分かる、基礎中の基礎ですね。
では、「-5」と「-1」ならどちらが大きいでしょう?
私が小学生の時は、「-5」と答えていました。
負の数を習っていませんし、数字が大きい方が大きいと考えていたからです。
負の数同士の大きさ比べは注意しないといけないのです。
では、数直線で確かめてみましょう!

数は右に行くほど大きくなっていきます。
数直線をみると、「-5」と「-1」なら「-1」の方が、右側にありますね!
つまり、「-1」の方が数は大きいということです!
まとめると、
①正の数同士の大小は、数字が大きい方が大きい。
②負の数同士の大小は、数字が小さい方が大きい。
ということになりますので、覚えておいてくださいね!
練習問題にチャレンジ
では、実際に絶対値の問題に挑戦してみましょう!
間違えても大丈夫です!
ただ、そのままにするのは絶対にやめてください!
上に戻って、しっかりと確認してくださいね!
【問題】
1.次の数の絶対値を求めよう。
9、-3、0、4、-8.3
2.絶対値が4になる数をすべて求めよう。
3.次の式を計算して求めよう。
|6|+|-2|-|5|=
【解答&解説】
1.次の数の絶対値を求めよう。
9、-3、0、4、-8.3
→9、3、0、4、8.3 となります。
絶対値は、「符号(+、-)を取った数値」でしたね!
ここで注意しないといけないのが、
0の絶対値は0であるということです。
2.絶対値が4になる数をすべて求めよう。
→-4、+4 となります。
符号を取った後が4になるのは、この2つだけですね!
3.次の式を計算して求めよう。
|6|+|-2|-|+5|=
→3 となります。
計算の順番としては、
①||を外した状態にする。(絶対値を求める。)
|6|→6
|-2|→2
|+5|→5
②外したものを式に置き換える。
6+2-5=3
オンライン家庭教師wamは絶対値と不等式以外の数学学習のサポートも充実しています無料相談はこちらから
絶対値を含む不等式の解き方を見ていこう!

ここまでは、絶対値の基本を見てきました。
次は、絶対値を含む不等式です!
不等式に絶対値が入ってくることで、難しく感じてしまいませんか?
進め方さえ覚えてしまえれば、あとは簡単です!
それに当てはめて、解いていけばいいだけですからね!
まずは、その進め方を確認していきましょう。
①絶対値記号(||)の中身が0以上か負の数かで場合分けをする。
②絶対値記号(||)をはずして、普通に方程式・不等式を解く。
③場合分けした条件を満たしているか確認する。
④解をまとめる。
この順番で、問題を解いていきましょう。
基礎問題
1.|X+4|=6
2.|X+2|=3X
…どうでしょうか。解けましたか?
では、進め方①~④に沿って解いていきます。
1.|X+4|=6
→(i)X+4≧0 すなわち X≧-4のとき…①
|X+4|=6
X+4=6…②
X=2
これは、X≧-4を満たす。…③
→(ii)X+4<0 すなわち X<-4のとき…①
|X+4|=6
-(X+4)=6 ←符号(-)をつける
-X-4=6…②
X=-10
これは、X<-4を満たす。…③
(i)(ii)より、X=2、-10…④
2.|X+2|=3X
→(i)X+2≧0 すなわち X≧-2のとき…①
|X+2|=3X
X+2=3X…②
X=1
これは、X≧-2を満たす。…③
→(ii)X+2<0 すなわち X<-2のとき…①
|X+2|=3X
-(X+2)=3X ←符号(-)をつける
-X-2=3X…②
X=-1/2
これは、X<-2を満たさない。…③
(i)(ii)より、X=1…④
この2問は基礎問題なので、数字を変えたりして慣れるまで解きましょう!
できるまでやれば、できる!!
できるようになれば、次は応用問題にチャレンジしよう!
応用問題
1.|X+6|<8
2.|X+4|≧5X
…基礎問題と違って、不等式になりましたね!
しかし!解く進め方は先ほどと同じで大丈夫です!
では、進め方①~④に沿って解いていきます。
1.|X+6|<8
→(i)X+6≧0 すなわち X≧-6のとき…①
|X+6|<8
X+6<8…②
X<2
X≧-6より、-6≦X<2…③
→(ii)X+6<0 すなわち X<-6のとき…①
|X+6|<8
-(X+6)<8 ←符号(-)をつける
-X-6<8…②
X>-14 ←両辺を-1で割るので、不等号の向きが変わることに注意!
X<-6より、-14<X<-6…③
(i)(ii)より、-14<X<2…④
2.|X+4|≧5X
→(i)X+4≧0 すなわち X≧-4のとき…①
|X+4|≧5X
X+4≧5X…②
X≦1 ←両辺を-4で割るので、不等号の向きが変わることに注意!
X≧-4より、-4≦X≦1…③
→(ii)X+4<0 すなわち X<-4のとき…①
|X+4|≧5X
-(X+4)≧5X ←符号(-)をつける
-X-4≧5X…②
X≦-2/3 ←両辺を-6で割るので、不等号の向きが変わることに注意!
X<-4より、X<-4…③
(i)(ii)より、X≦1…④
不等式が入ることで、より数直線のイメージが必要になりますね!
イメージよりも書いた方が…。という人は、ぜひそうしましょう!
では最後に、証明問題です!
証明問題
次の不等式を証明しよう。
|X+Y|≦|X|+|Y|
この問題では(右辺)の方が大きくなることが分かるので、(右辺)²-(左辺)²を考えます。
|X|+|Y|≧0、|X+Y|≧0より、平方の差を考えると、
(|X|+|Y|)²-|X+Y|²
右の部分の展開は絶対値の性質|X+Y|²=(X+Y)²より、
=|X|²+2|X||Y|+|Y|²-(X²+2XY+Y²)
また、|X|²=X²、|Y|²=Y²、|X||Y|=|XY|より、
=X²+2|XY|+Y²-X²-2XY-Y²
=2|XY|-2XY
=2(|XY|-XY)
ここで、|X|-X≧0より
=2(|XY|-XY)≧0
よって、
(|X|+|Y|)²-|X+Y|²≧0
ゆえに、
(|X|+|Y|)²≧|X+Y|² が成り立つ
ここで、X≧0、Y≧0のとき、X²≧Y²⇔X≧Yより
|X|+|Y|≧|X+Y|
したがって、
|X+Y|≦|X|+|Y|
まとめ
さて、ここでは絶対値と不等式について学んできました。
苦手は克服できましたか?
学習は振り返ることも大切ですが、その時にはできるまでやってみましょう!
絶対値が出てきたときには、必ず数直線をイメージしましょう。
書いてみて、目で確認するとより分かりやすいですね。
急がなくていいので、しっかりと理解していきましょう!
■ この記事の監修者

オンライン家庭教師WAM講師。「数学・化学」を中心に全科目対応。
高3の夏にD判定を取るも、自己分析を行い自分の弱点を知ることで、冬にA判定を取ることができ、第一志望校に現役合格。中学、高校共に公立出身であることを生かして、公立中学、高校での勉強法の指導も可能。


















