合同と相似とは？　演習問題にチャレンジ！

こんにちは！オンライン家庭教師WAMです(^^)/

 

「三角形の合同と相似」

いきなり説明してほしいと言われた際、皆さんは正しく答えることができますか？

「どっちも似たような意味じゃないの？」「一体なにが違うの？」「そもそも合同と相似ってなに？」

 

高校受験の範囲でもある「三角形の合同と相似」

受験生なら押さえてきたいポイントです！

今回は、「三角形の合同と相似」の意味と条件について例題も用いて解説していきます。

 

合同とは

合同の意味・条件

合同とは、２つの図形の形と大きさが『完全に』一致することを表しています。

分かりやすく説明すると、２つの図形を重ね合わせて形も大きさもピッタリ同じになることです。

 

 

説明だけを見るとかなり簡単に思えますが、実際に問題を解く際は教科書やプリントに描いてある図形を動かすことはできませんよね。

それでは、一体どうすれば合同であることを証明できるのでしょうか？

 

正解は、合同である条件を探し出せばいいのです。

三角形の合同の条件は以下の3つとなっています。

 

・3組の辺がそれぞれ等しい　　　　　　　　　　…条件①

・2組の辺とその間の角がそれぞれ等しい　　　　…条件②

・1組の辺とその両端の角がそれぞれ等しい　　　…条件③

 

この3つの合同条件のうち1つでも成り立っている場合は、それらの三角形は合同であるということが証明できます。

それでは条件①から図を用いて説明していきますね。

 

条件①　3組の辺がそれぞれ等しい

 

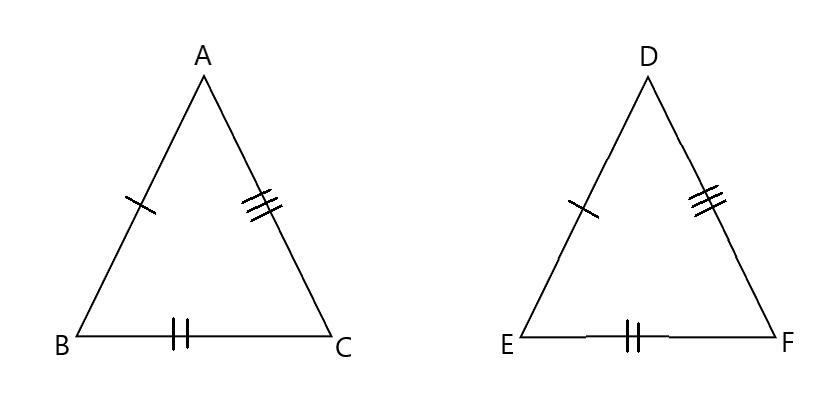
上記の図の場合、AB=DE,BC=EF,CA=FD で3組の辺がそれぞれ等しいことから合同といえます。

ちなみに合同であることにより、∠A=∠D,∠B=∠E,∠C=∠F であることもわかりますね！

 

条件②　2組の辺とその間の角がそれぞれ等しい

 

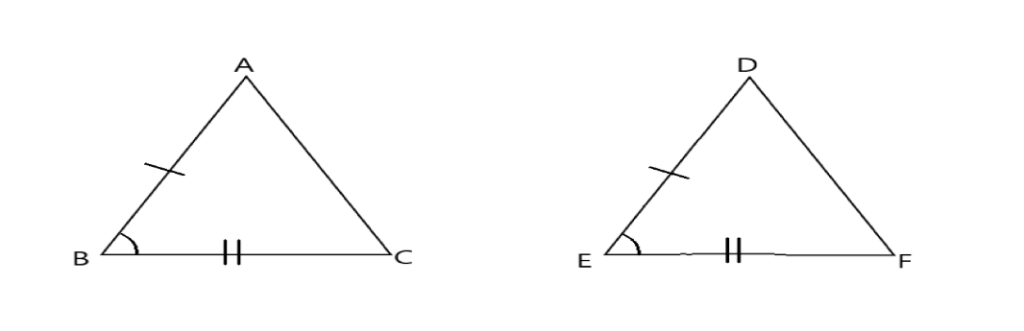
上記の図の場合、AB=DE,BC=EF,∠B=∠E で2組の辺とその間の角がそれぞれ等しいことから合同といえます。

条件①でも説明したように、合同であることにより、CA=FD,∠A=∠D,∠C=∠F ということも分かります。

 

条件③　１組の辺とその両端の角がそれぞれ等しい

 

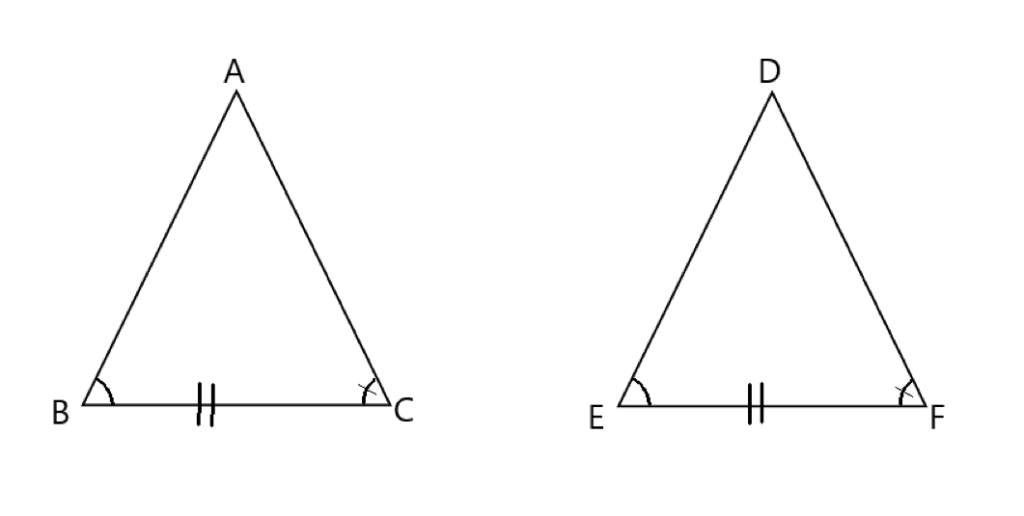
上記の図の場合、BC=EF,∠B=∠E,∠C=∠Fで１組の辺とその両端の角がそれぞれ等しいことから合同といえます。

この時も合同であることにより、AB=DE、CA=FD,∠A=∠Dということも分かります。

 

 

ここで1つ、よく間違いが起こる箇所があります。

それは条件③なのですが、1組の辺とその【両端】の角がそれぞれ等しいを1組の辺と【2組】の角がそれぞれ等しいと誤って覚えてしまうことです。

この間違いをしてしまうと比較している三角形は合同ではなくなってしまいます。

これでは証明もできないので、間違えて覚えてしまわないよう注意しましょう。

 

 

相似とは

相似の意味・条件

相似とは、同じ形のまま拡大や縮小をした図形であることを指しています。

分かりやすく説明すると、比較する図形がもう一方の図形より大きかったり小さかったりしても『形は同じである』ということです。

この相似の場合も、教科書やプリントを拡大や縮小をすることはできないので、合同で説明した様に相似の条件を探しだします。

 

相似の条件も3つとなっています。

 

・3組の辺の比が、すべて等しい　　　　　　　　　…条件①

・2組の辺の比とその間の角がそれぞれ等しい　　　…条件②

・2組の角が、それぞれ等しい　　　　　　　　　　…条件③

 

上記の3つの条件のうち1つでも当てはまっている場合は、相似と証明することができます。

合同も相似も、条件を覚えるだけでは問題を解くことができません。

特に、相似はよく間違える方も多いので、どういうときにこの条件を使うのか、などしっかり理解しながら覚えていきましょう。

それでは条件①から説明していきますね。

 

条件①　3組の辺の比が、すべて等しい時

 

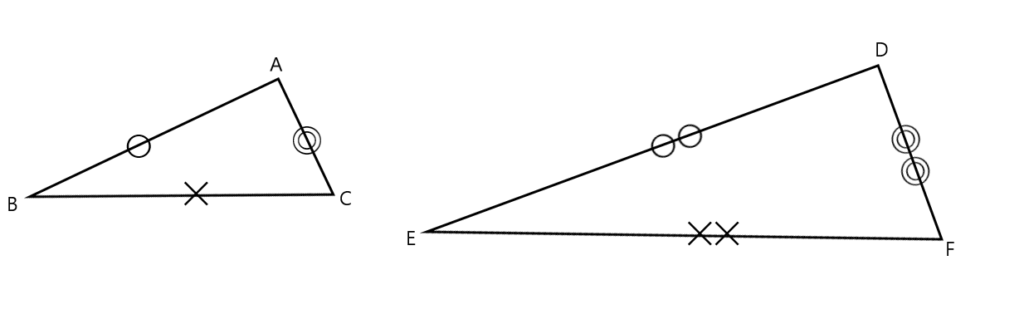
上記の図の時、AB:BC:CA=DE:EF:FD=○:×:◎より相似となります。

 

この相似条件は、AB:DE=BC:EF=CA:FDと言い換えることもできます。

上図の場合、AB:DE=BC:EF=CA:FD=1：2　より相似となりますね！

 

条件②　２組の辺の比とその間の角がそれぞれ等しい

 

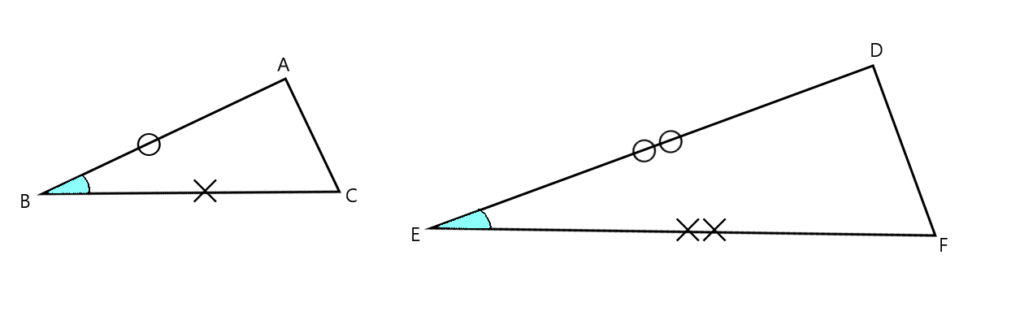
上記の図の場合、まず重要となるのが「その間の角」というところですね。

2辺の間の角でない場合は相似とは言えません。

AB:DE=BC:EF=1：2 かつ、その2辺の間の角 ∠B=∠E より、相似となります。

 

条件③　２組の角が、それぞれ等しい時

 

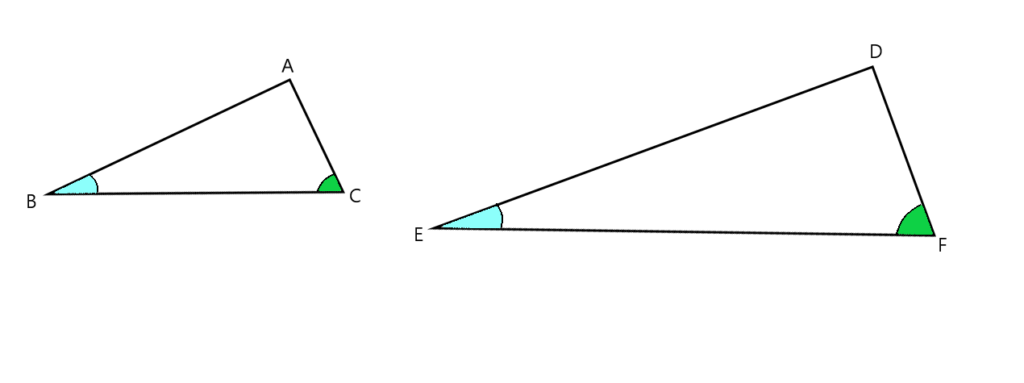
上記の図の場合は、∠B=∠E かつ ∠C=∠F より、相似となります。

条件①や②のように辺の比を考えなくていい分、同じ角度の角を2組見つけるだけで証明ができるので、3つの条件のうち最も分かりやすいかと思います。

 

ちなみに余談になりますが、相対比という言葉はみなさん聞いたことはありますか？

「相似である2つの図形の対応する辺の長さの比」を相似比といいます。

つまり、最初の方で説明した合同な図形は相対比が1：1の相似な図形と考えることもできます。

 

 

例題

例題１

下の図で、合同な三角形はどれとどれですか。

3組選び、それぞれ記号≡を使って答えなさい。

また、その時に使った三角形の合同条件をいいなさい。

 

 

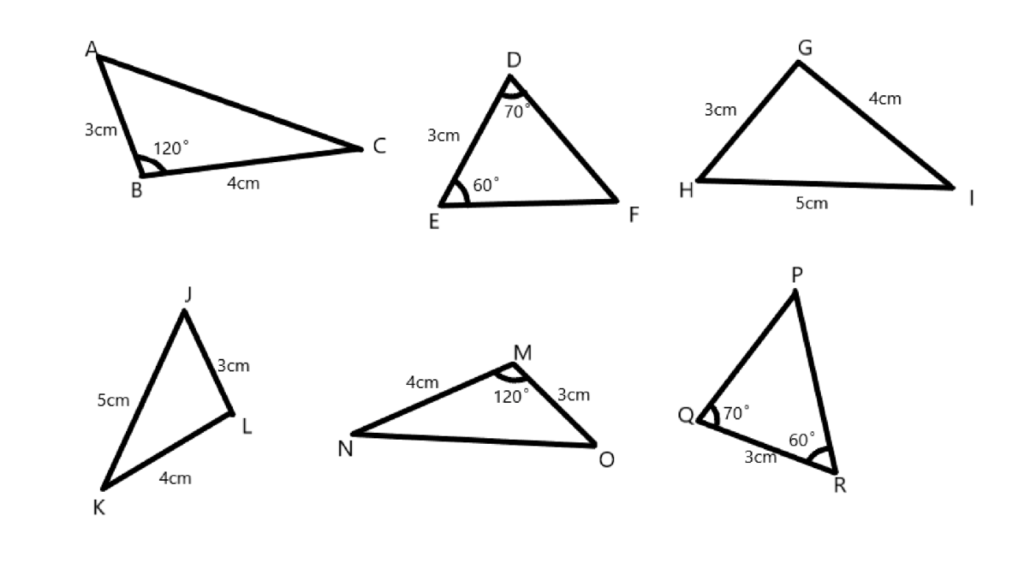
解き方

答えを先に出しますね。

△ABC=△OMN                  2組の辺とその間の角がそれぞれ等しい。

△DEF=△QRP                   1組の辺とその両端の角がそれぞれ等しい。

△GHI=△LJK                    3組の辺がそれぞれ等しい。

 

みなさん答えは合っていましたか？

それでは分からなかった方は△ABCと合同になるものを一緒に探していきましょう。

 

まずは各々の図形の情報をしっかりと確認しましょう。

例えば△ABCは、辺ABが3㎝、辺BCが4㎝、そしてその2組の辺とその間の角が120゜ということが分かりますね。

ここまで分かれば、あとは同じ条件のものを探すだけでいいので簡単ですね。

つまり、同じ条件のものは△OMNです。

 

ここで1つ注意点があります。

△ABC≡△MNOと書いた方はいませんか？

合同や相似の回答でよくある間違いが、対応するアルファベットの順番です。

例えば△ABCの頂点Aにあたる△OMNは頂点Oになります。

この順番が違ってしまうと減点の対象となるため注意しましょう。

せっかく問題の答えまで出すことができたのに、書き方で減点をされるともったいないですからね！

 

例題２

下の図の中には相似な三角形が3組あります。

記号で答えなさい。

また、その時に使った相似条件も答えなさい。

 

 

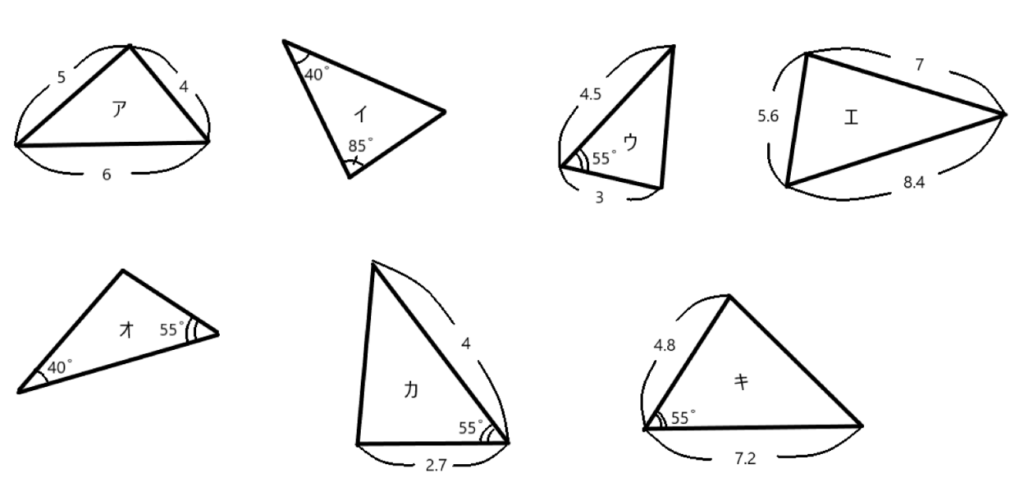
解き方

答えを先に出しますね。

アとエ   …　3組の辺の比がそれぞれ等しい

イとオ   …　2組の角がそれぞれ等しい

ウとキ　…　2組の辺の比とその間の角がそれぞれ等しい

 

みなさん答えは合っていましたか？

それでは一緒にアとエが相似なのか確かめていきましょう。

 

合同の例題と同じように、まずは図形の情報をしっかりと確認しましょう。

アの1番短い辺は4に対しエの1番短い辺は5.6

アの1番長い辺は6に対しエの1番長い辺は8.4

こういった情報をもとに相似比を作ってみましょう。

4：5.6=6：8.4=5：7

アの辺をすべて1.4倍したものが、エの図形になることが分かりましたね。

よって、アとエは3組の辺の比がそれぞれ等しい相似な図形であるといえますね。

 

 

まとめ

合同と相似の説明は以上になります。

一見面倒くさそうに思える合同と相似ですが、やっていくことはいたって単純です。

 

まずは、三角形の合同になる3つの条件・相似になる3つの条件をしっかり覚えましょう。

覚えたうえで、例題のような簡単な問題から確実に解いて力をつけていくことが大切です。

例題で上げた注意点のような、アルファベットの順番を間違えてしまうという凡ミスを完璧になくしていきます。

問題もなく解けるようになったら、次の証明に挑戦していきましょう！