フィボナッチ数列と黄金比～自然界から金融まで～

こんにちは！オンライン家庭教師WAMです(^^)/

今回は【フィボナッチ数列と黄金比～自然界から金融まで～】についてお話します。

 

まずは、フィボナッチ数列というものを紹介し、美しい比率と言われている黄金比について、さらにフィボナッチ数列との関わりを説明していきます。

 

最後に、フィボナッチ数列や黄金比の自然界との関わりや利用について書いていきます。

 

フィボナッチ数列とは

数列とは

「数列」というのは数を並べたものです。

下にいくつか数列を書いてみます。

どのような規則で数字が並んでいるのか、考えてみてください。

下の方に答え合わせがあります。

 

①1 , 1 , 1 , 1 , 1 , ・・・

 

②1 , 3 , 5 , 7 , 9 , ・・・

 

③24 , 12 , 6 , 3

 

④5 ,12 , 7 , 13 , 8 , 15 , 22 , 31

 

 

規則の答え合わせ

①1を並べたもの

②奇数を並べたもの（1から始めて2ずつ足していったもの、という答えでも良いでしょう）

③24を2で割っていったもの

④適当に思いついた数を並べたもの

 

最後の④については怒られそうな答えですが、これも立派な数列です。

 

フィボナッチ数列

さて、フィボナッチ数列についてですが、「フィボナッチ」というのはイタリアで活躍されていた数学者の、レオナルド・フィボナッチさんのことを指しています。

 

（レオナルド・フィボナッチの肖像画　出典：Wikipedia）

 

「算盤の書」という書物でフィボナッチ数列について言及したことにより、その数列にフィボナッチさんの名前が付けられました。

 

フィボナッチ数列とは下のような数列です。

 

1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , ・・・

 

この数の並びの規則が分かるでしょうか？（先程の問題とは違い、この数列にはちゃんと規則があります！）

 

答えは、「前の2項を足した数字が次の項になる」というものです。

ここでいう「項」とは、並んでいる各数字のことを指しています。

 

例えば、最初の項の「1」と2番目の項の「1」を足すと、3番目の項の「2」になります。

また、2番目の項の「1」と3番目の項の「2」を足すと、4番目の項の「3」となっています。

 

これがフィボナッチ数列の規則です。

 

また、フィボナッチ数列に出てくる数1,2,3,5,8・・・は、「フィボナッチ数」と呼ばれています。

 

 

フィボナッチ数列と黄金比

では、このフィボナッチ数列の面白い点はどこにあるのでしょうか。

 

フィボナッチ数列について、後の項を前の項で割っていってみましょう。

出てきた値は小数第３位まで残して四捨五入します。

 

フィボナッチ数列は

1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , ・・・

でした。

 

1÷1=1

2÷1=2

3÷2=1.5

5÷3=1.667

8÷5=1.6

13÷8=1.625

21÷13=1.615

34÷21=1.619

55÷34=1.618

89÷55=1.618

144÷89=1.618

 

とりあえずここまでにしておきましょう…

 

「後の項÷前の項」という計算をしていくと、その値が段々と「1.618」という値から変わらなくなりました。

この1.618・・・という値こそ、「1：1.618・・・」で表される比、「黄金比」に出てくる数字です。

黄金比は美しい比と言われており、黄金比を元に作成された美術作品などもあります。

また、後述しますが、自然界にも黄金比やフィボナッチ数がよく見られると言われています。

ちなみに、この黄金比は無理数と呼ばれる、小数が無限に続く数字です。

 

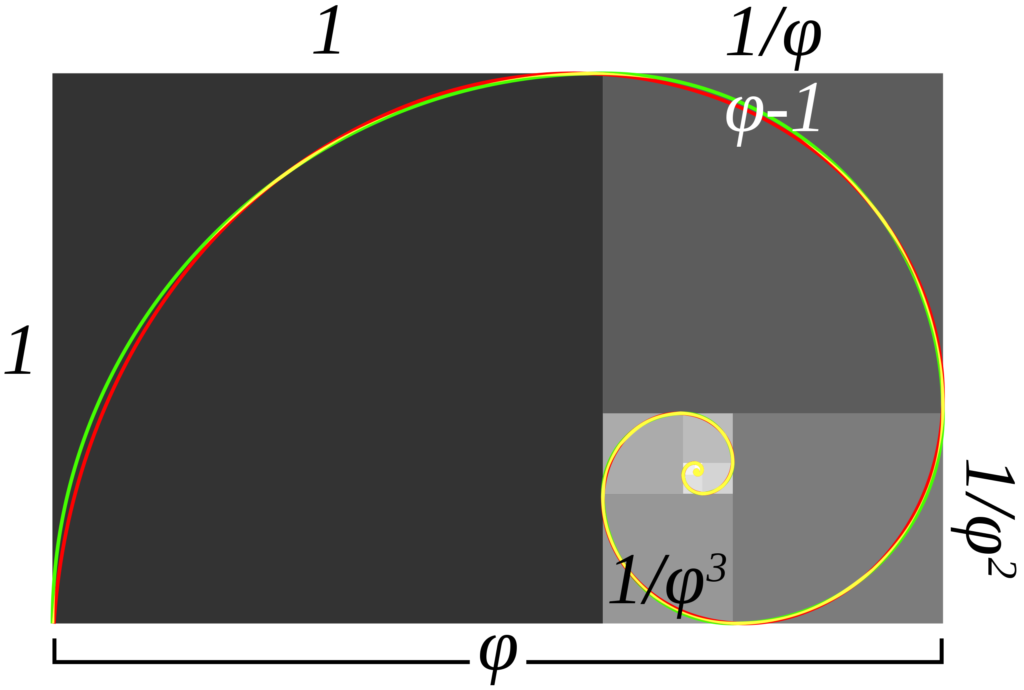
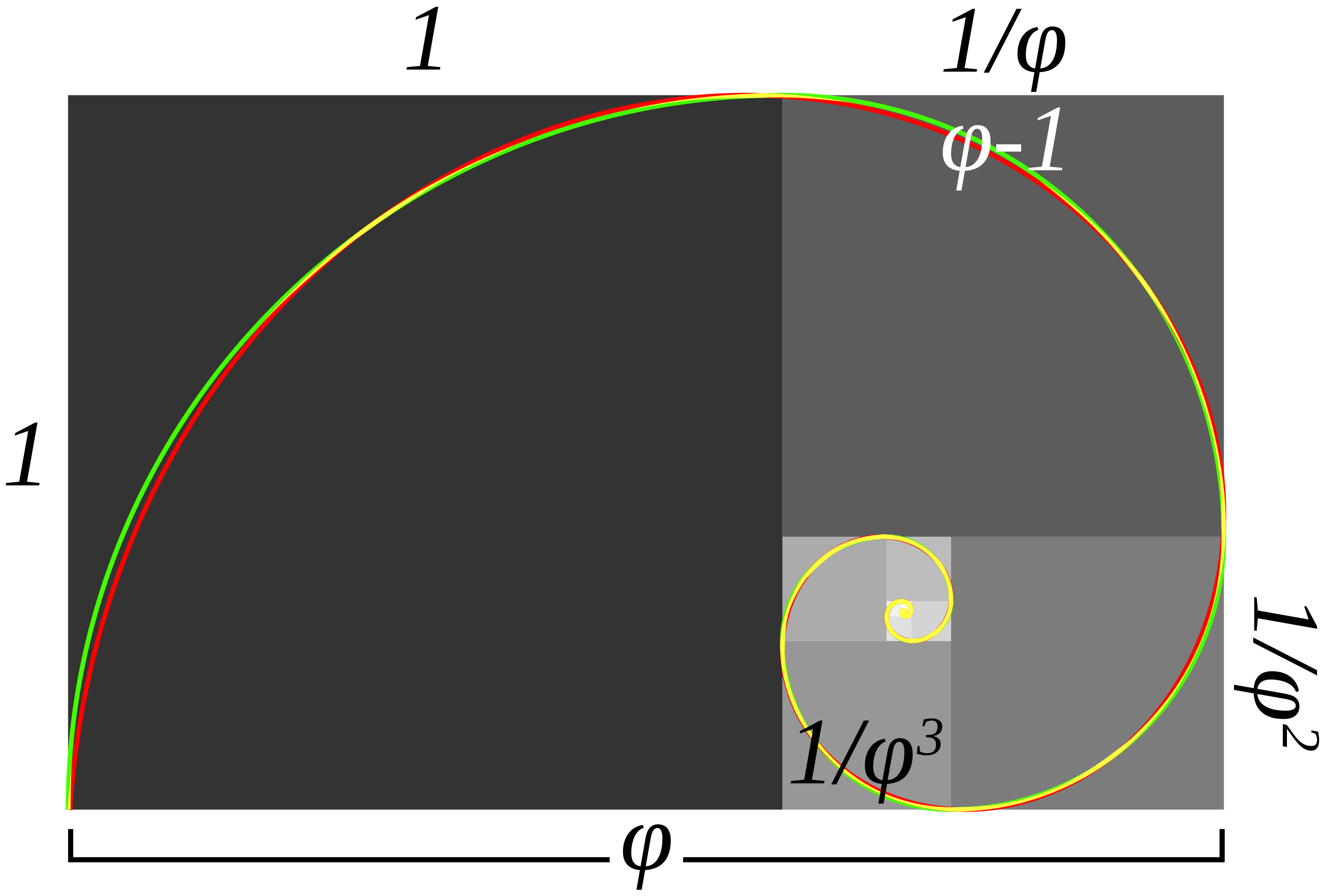
（黄金長方形　出典：Wikipedia）

 

では、この1.618・・・を分数と平方根を用いて正確に表記してみましょう。

中学校3年生の皆さんは、もう学校で平方根を習ったでしょうか。

平方根をご存知の方は、下の数が大体どのくらいの値になるか、計算してみてください。

 

 

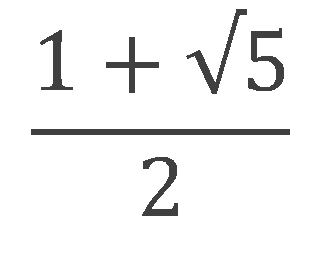
まだ平方根を習っていない方は、上の〈√5〉を「2.236」という数字に置き換えて計算してみてください。

 

計算すると・・・

 

 

 

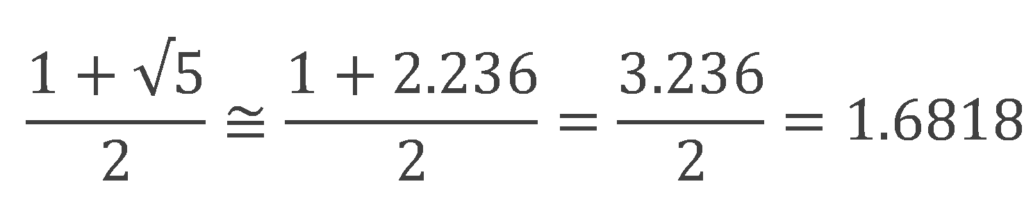
となりました。

 

つまり、フィボナッチ数列から出てきた「1.618・・・」を分数と平方根で表すと、

 

 

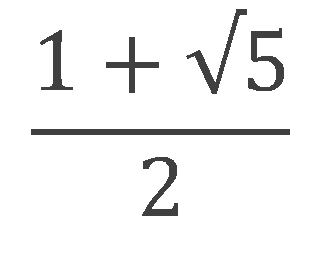
という数字になります。

 

 

フィボナッチ数列の漸化式と特性方程式

 

では、この平方根の入った数字がどういった数字なのか見ていきましょう。

 

ここからは高校数学の話になります。

できるだけ分かりやすく解説していきますが、興味の無い方は黄金比の利用まで飛ばして読んでください。

 

先ほどの黄金比を表す数字は、フィボナッチ数列の「漸化式」について「特性方程式」を解いて導出することができます。

 

さて、「漸化式」と「特性方程式」という難しい言葉が出てきました。

どれも高校で習う数学Bの「数列」分野に出てくる言葉です。

ひとつずつ説明していきます。

 

漸化式

「漸化式」というのは数列の項と項の関係を表す式です。

フィボナッチ数列の漸化式は下のような式になります。

 

 

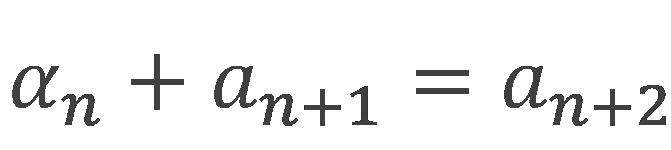
難しそうな式ですが、nは番号を表していて、2つ並んだ「n」番目の項と「n+1」番目の項を足すと、その次の「n+2」番目の項になるということを表しています。

 

1+1=2

1+2=3

2+3=5

・

・

・

 

などの関係を、文字を使ってまとめて表したものが上の漸化式です。

 

特性方程式

次に「特性方程式」というのは、数列をどんどん先に進めていったとき、後の項を前の項で割ったときの値、要は先程の

 

1÷1=1

2÷1=2

3÷2=1.5

5÷3=1.667

8÷5=1.6

・

・

・

 

を計算していくと、どのような値に近づくのかを求めるための方程式です。

 

先程の漸化式

 

 

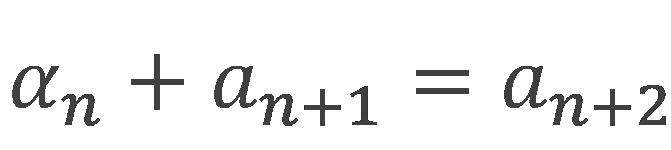
から特性方程式を作ると、

 

 

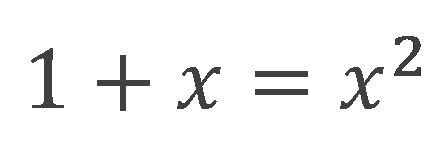
という方程式ができます。

 

特性方程式の作り方は参考書に譲ることにして、この方程式は中学3年生の「2次方程式」分野で解くことができ、答えは

 

 

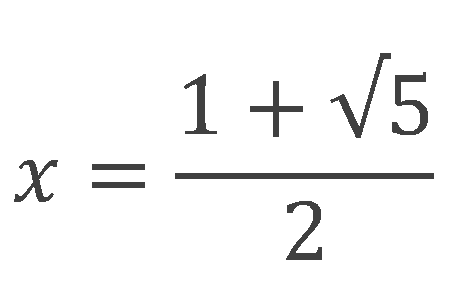
となります。

 

＋の方の解が先程の黄金比に出てきた数字、

 

 

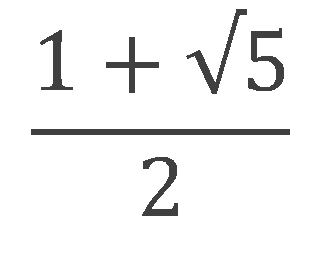
となります。

 

 

フィボナッチ数列の一般項

 

さて、数列には一般項というものがあります。

一般項とは、その数列の第n項目がどのような値になるかを表したものです。

 

例えば、

 

 

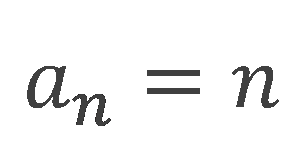
という一般項の数列を考えます。

nに1～5までの数字を代入してみると、

 

 

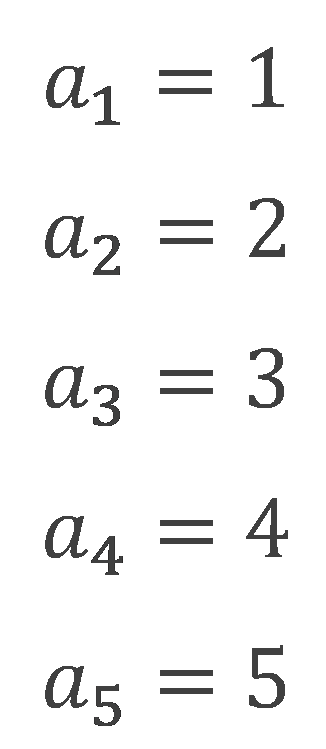
となるので、この一般項の数列は、

1,2,3,4,5,・・・

という数列になります。

 

もう一つ例を出してみましょう。

 

 

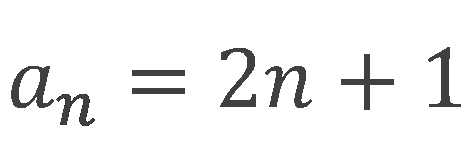
という一般項はどのような数列を表しているでしょうか。

nに1,2,3,4,5・・・を代入して計算していくと、

 

 

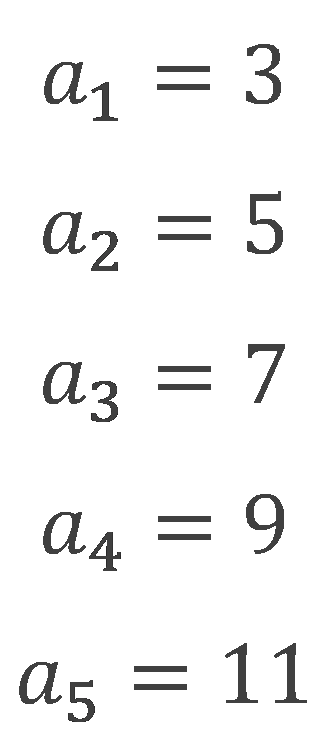
となるので、この一般項の数列は、

3,5,7,9,11・・・

となります。

 

 

数列の一般項が分かると、その数列の好きな番号の項が分かるようになります。

例えば先程の

 

 

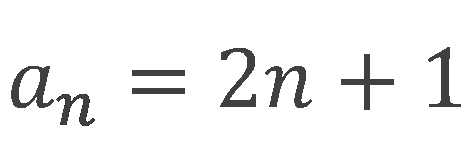
という数列で、10番目の項の値を求めたいと思えば、nに10を代入して、

 

 

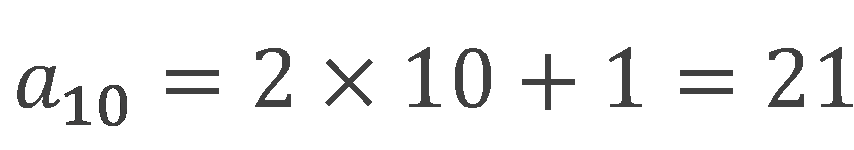
となります。

 

 

それでは、フィボナッチ数列の一般項はどのようになるのでしょうか。

 

実際の導出方法は高校の参考書などに譲るとして、一般項の形は、

 

 

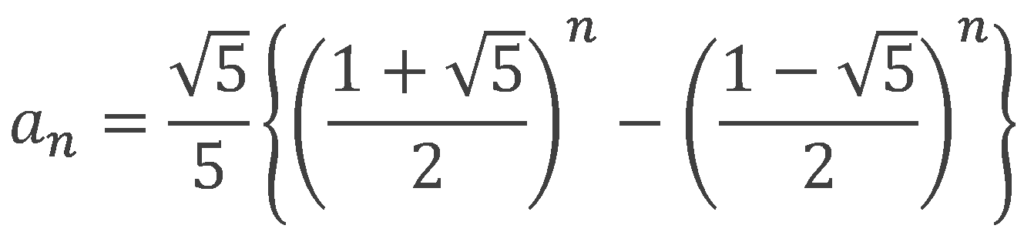
となります。

なにやらとんでもない数字が出てきました。

 

せっかくなので、n=1を代入して計算し、フィボナッチ数列と合うか見てみましょう。

フィボナッチ数列の1番目の項は「1」だったので、上の式にn=1を代入し、答えが1になることを確かめます。

 

 

 

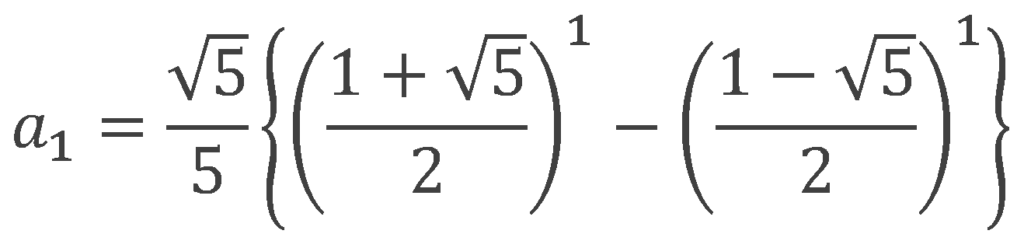
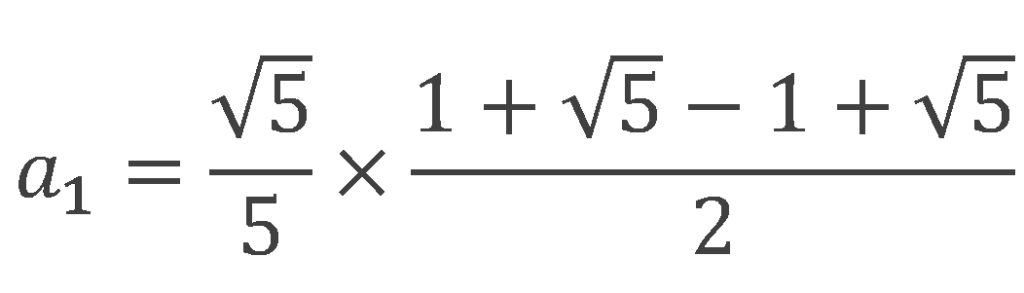
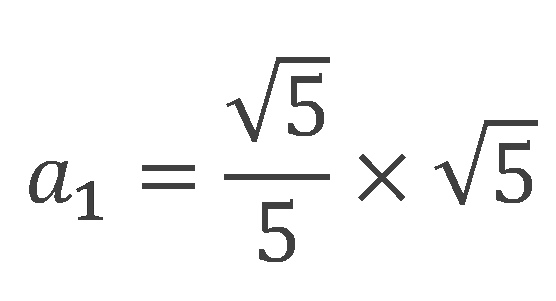
確かに一番目の項が1になることが分かりました。

計算できそうな方は、2番目、3番目と計算してみてください。

 

 

一般項の中に平方根が出てきているのに、数列自体は

 

1,1,2,3,5,8,13,・・・

 

と自然数が並んだ形になっています。

 

これはとても不思議なことではないでしょうか。

 

 

フィボナッチ数と黄金比の利用

自然界にあると言われている

例えば、花の花弁の数を数えると、3,5,8などのフィボナッチ数になっていることが多いそうです。

実際に確認してみましょう。

 

 

桜の花弁は5枚です。

 

 

菖蒲の花弁は3枚です。

 

確かに、今見た花たちは花弁の数がフィボナッチ数になっています。

 

花弁の数がフィボナッチ数になっていないものもあります。

 

 

ニワゼキショウという花ですが、花弁は6枚です。

花弁の数は、必ずしもフィボナッチ数になるわけではないようです。

 

どんなことも疑ってみよう

ところで、この項目の冒頭で、花弁の数がフィボナッチ数になっている植物が多いと書きました。

それを読んだとき、読者の皆様はどのように思われたでしょうか。

 

「それはすごい」と思ったか、「ふーん」とあまり興味をひかなかったか、はたまた別の反応をされたかもしれません。

 

科学の勉強をする上で大事なことは、こういった話を聞いたときに、「そうなんだ」と手放しで正しいと思うのではなく、

「本当にそうなのだろうか」

「実際に確かめてみよう」

「花弁の数がフィボナッチ数になっている植物が多いのだとしたら、何故そうなっているのか考えてみよう」

「そもそも花弁の数がフィボナッチ数になっていることが多いというのは、どこの情報なのだろうか」

というように、疑問を持ちながら思考し調べていくことが、科学的なリテラシーや思考力を高める秘訣だと思います。

 

また、花弁の数について考える際、もしかしたら生物学の知識が役に立つかもしれません。

分からないことについて考えるとき、思考のための武器となるのが学校の授業で習う事柄です。

義務教育の範囲内でも、意外と思考の手助けになる事を習っているものです。

高校や大学で専門的な事を習えば、なおさら未知のものを理解するための武器が増えていきます。

学校の勉強は何に役立つのか分かりません。

だからこそ、未来への投資だと思って今からしっかり勉強していきましょう。

 

….話が逸れてしまいました(;´･ω･)

 

金融界のフィボナッチ数

最後にもう一つ、実際に黄金比が使われている例を挙げて終わりにしましょう。

 

投資・金融の分野で「フィボナッチ・リトレースメント」と呼ばれているものがあります。

これは、株でも為替でもいいのですが、その値動きをフィボナッチ数列から導き出される黄金比で予測しようという方法です。

 

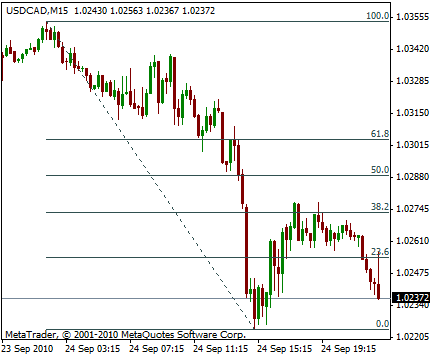
（フィボナッチ・リトレースメント　出典：Wikipedia）

 

もしも株や為替の値動きを予測できるならば、安いところで買って高くなったら売り、確実に儲けを出すことができます。

このような方法があることについて、ここまで読んでいただいた皆様はどのように思われるでしょうか。

まず、もしも確実に未来予測のできる方法があるとしたら、この方法を使ったみなさんが大金持ちになり、確実に儲かる方法として話題になっているはずです。

 

ところが現実はそうではない以上、フィボナッチ・リトレースメントは確実に未来を予測できる方法ではないということになります。

確実に未来を予測できないならば、この方法に意味はないのでしょうか。

 

しかしながら、そうとも言い切れません。

 

確実な予測はできなくても、値動きが黄金比に従う“傾向がある”ならば、何度もフィボナッチ・リトレースメントに従って株の売買を行えば、最終的に儲けが出るかもしれません。

ただ、それには“傾向がある”ことを過去のデータに当てはめて確かめる必要があります。

傾向があることを確かめるには、何回・何十回調べるだけではだめで、何百・何千回と当てはめをする必要があります。

 

大事なお金を投資するならば、尚更慎重に確かめてみなければいけません。

もし、他の人が確かめて「そういう傾向があった」と言ったとしても鵜呑みにすることはできません。

何回試したのか、どんな方法で調べたのか、そもそも本当に確かめたのか分からないからです。

 

勉強も同じで、自分で納得のいくまで調べて考えることで、ようやくその知識や方法は自分の物となっていきます。

身につけるための近道はなく、何百・何千回と問題を解いて、一つ一つ自分の物にしていくしかありません。