実数を分類しよう

こんにちは!オンライン家庭教師WAMです(^^)/
実数とは何かわかりますか?
数学の初歩として、実数が何かをきちんと理解しておくことはとても大切です。
また、絶対値の概念も今後数学を学んでいく上で役に立つ知識です。
今回は、実数に焦点を当てて詳しく解説していきたいと思います。
Contents
実数とは
実数とは
実数は、有理数と無理数に分けられます。
また、有理数は整数・有限小数・無限小数に分けられ、さらに、整数は正の数・0・負の数に分けられます。
これらの数は、以下のように分類することができます。
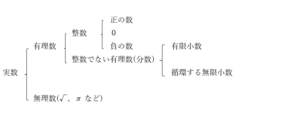
ここで注目する言葉は、有限小数と無限小数です。
有限小数は、0.75や0.8のように小数点以下を有限な数字で表すことができます。
逆に、無限小数は小数点以下の数字が無限に続きます。
次に、無限小数の中も分類してみましょう。
無限小数の中でも、
0.2323232323…
というように同じ数字が循環するものを循環小数
0.87676889985…
というようにランダムな数字が続く場合は無理数になります。
有理数とは
ここで重要になってくる有理数について解説していきます。
有理数は、分数で表すことのできる数を示します。
整数は、例えば3= 3 / 1 のように分数で表すことができます。
また、有限小数、循環小数も分数で表すことができます。
有限小数については0.9 = 9 / 10 、0.98 = 98 / 100 のように分数で表すことができます。
循環小数の分数への変換の仕方は、後程説明していきます。
このように、有理数の共通する特徴は「分数で表すことができる」ということが挙げられます。
無理数とは
逆に、分数で表せない場合について考えていきましょう。
分数で表せられないものを無理数と言います。
無限小数や √ 、π などが当てはまります。
√2= 1.41421356…
と無限に続いていき、かつ循環しない小数を分数で表すことができません。

例題にチャレンジ
では、次の数の中から有理数を選んでください。
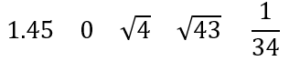
解き方のポイントは、『分数で表すことができるか』です。
もっと言うと、無理数は √ と π とランダムに続く無限小数だけなので、それ以外で考えていきます。
そこでまずは
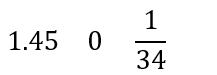
が答えになることがわかります。
次に、
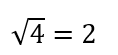
なのでこれも有理数に含まれます。
したがって答えは
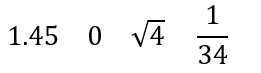
となります。
絶対値とは
絶対値とは
絶対値とは、「数直線上での原点からの距離」を表します。
例えば2は、0からの距離が2なので、絶対値も2となり、
-2でも0からの距離は2なので、絶対値は2になります。
絶対値は、距離を表すので負の数になることはありません。
問題においては、『その数の符号をとった数』と覚えておいてよいと思います。
絶対値の表し方
絶対値を表すときは | -3 | のように表します。
この記号で表されているときは、「絶対値」を表しているのかと理解するようにしましょう。
例題にチャレンジ
では、ここまで学んだことを生かして例題を解いていきましょう。
⑴ 次の数の絶対値を答えなさい。
①8 ②-9 ③0
答えは、符号をとればよいので
①8 ②9 ③0
となります。
⑵ 絶対値が4以下になる整数を小さいほうから順に答えなさい。
「以下」なので-4、4も含まれます。
これらよりも絶対値が小さくなるような数は
-4、-3、-2、-1、0、1、2、3、4
になりこれが答えになります。
⑶ 以下の式を計算しなさい。
2 + | -5 | + | -2 |
絶対値は符号をとればよいので
2 + | -5 | + | -2 |
= 2 + 5 + 2
= 9
となります。
循環小数を分数で表そう
循環小数とは、0.878787878…のように同じ数の羅列が続く小数です。
実はこの循環小数は、分数で表すことができるんです。
例えば、1.44444444…
この小数について考えていきましょう。
x=1.4444444…として10倍します。
10x=14.44444444…と表すことができます。10倍したので位が1つずれています。
次に、この2つの式の差を求めてください。

と表すことができます。
次に
0.123123123…
この場合について考えていきましょう。
この場合は123123…の部分を消したいのでこの部分が小数点以下になるようにします。
そのように考えると

小数点以下をそろえるように、循環している数字の個数を a としたら 10 ^ a × xと x の差を考えます。
では、例題を何問か解いてみましょう。
① 0.1212121212…を分数に直しなさい。
この場合は、12が循環しているので10²つまり100xを考えます。

② 0.9876598765…
この場合も同様に考えていきます。

桁が増えても解き方は同じです。
基本に則って解いていきましょう。
まとめ
今回は、数学の基本中の基本である実数について解説してきました。
有理数、無理数は区別できるようになりましたか?
また、循環小数の問題はテストで頻出なので解き方をマスターしておきましょう。
まずは基本から正しく理解できるように繰り返し練習しておきましょう。



















