苦手克服　二次関数の解き方（基本編）

こんにちは！オンライン家庭教師WAMです(^^)

 

高校入試や大学入試（共通テスト）では頻出となっている二次関数。

みなさんは理解できていますか？

苦手だという人も多いかもしれません。

今回は基本編ということで、二次関数の中でも中学校で習う基本的な y=ax²（二乗に比例する関数）について確認していきましょう。

 

一次関数は理解できていますか？

関数とは？

はじめに関数ってなんだかわかりますか？

言葉の意味を理解せずに使っている方も多いかもしれません。

関数とは、「ともなって変わる2つの変数x，yがあって、xの値を決めると、それに対応してyの値がただ１つ決まるときyはxの関数であるという」（参照：未来へひろがる数学１，啓林館）

 

ということです。

わかりやすいように例を出して考えましょう。

 

「縦の長さがx cm、横の長さが６ cmの長方形の面積y ㎠」

 

これはxの値が３だとしたらyの値は18とただ一つに決まります。

xの値が3以外だとしてもyの値はただ一つに決まるので、この場面では、長方形の面積は縦の長さの関数であるといえます。

また、面積を決めると縦の長さも一つに決まるので、縦の長さは長方形の面積の関数であるともいえます。

 

一次関数とは？

では一次関数とはどのようなものでしょうか？

一次という言葉がついていますのでもちろん一次式の形になっています。

 

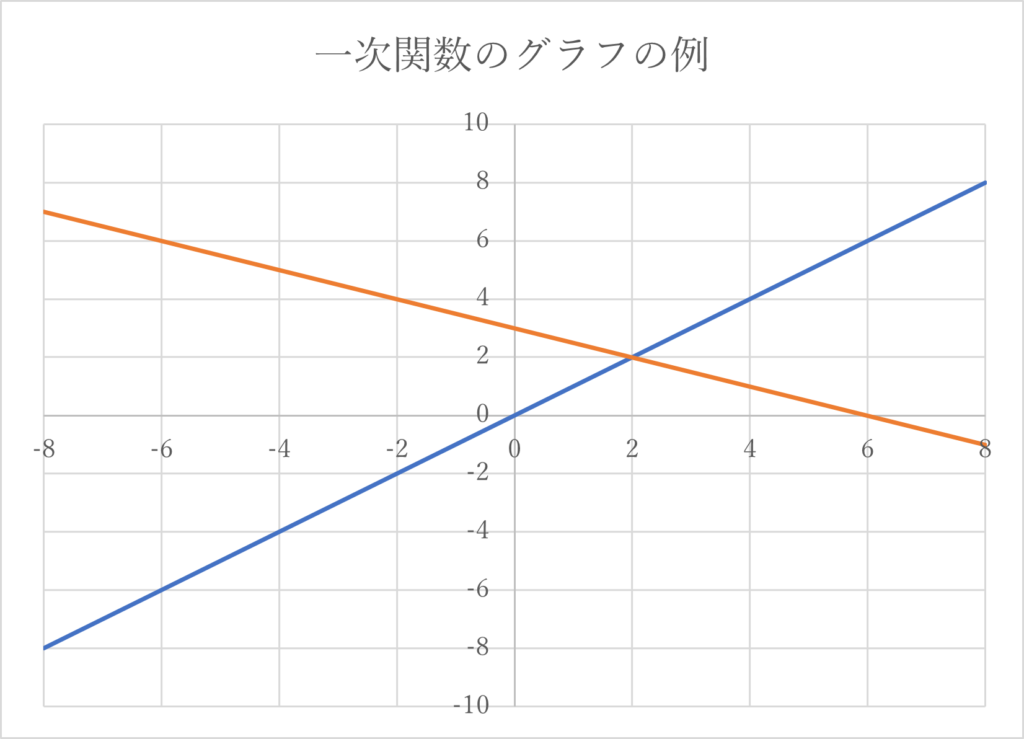
「yがxの関数で、ｙ＝2x+8 、y=5x のように、yがxの一次式で表されるとき、yはxの一次関数であるという」

 

一次関数は「y=ax+b, a,b は定数」と表すことができます。

 

 

二次関数とは？

それでは二次関数とはどのようなものでしょうか。

一次関数の時と同様に考えると以下のような定義になります。

 

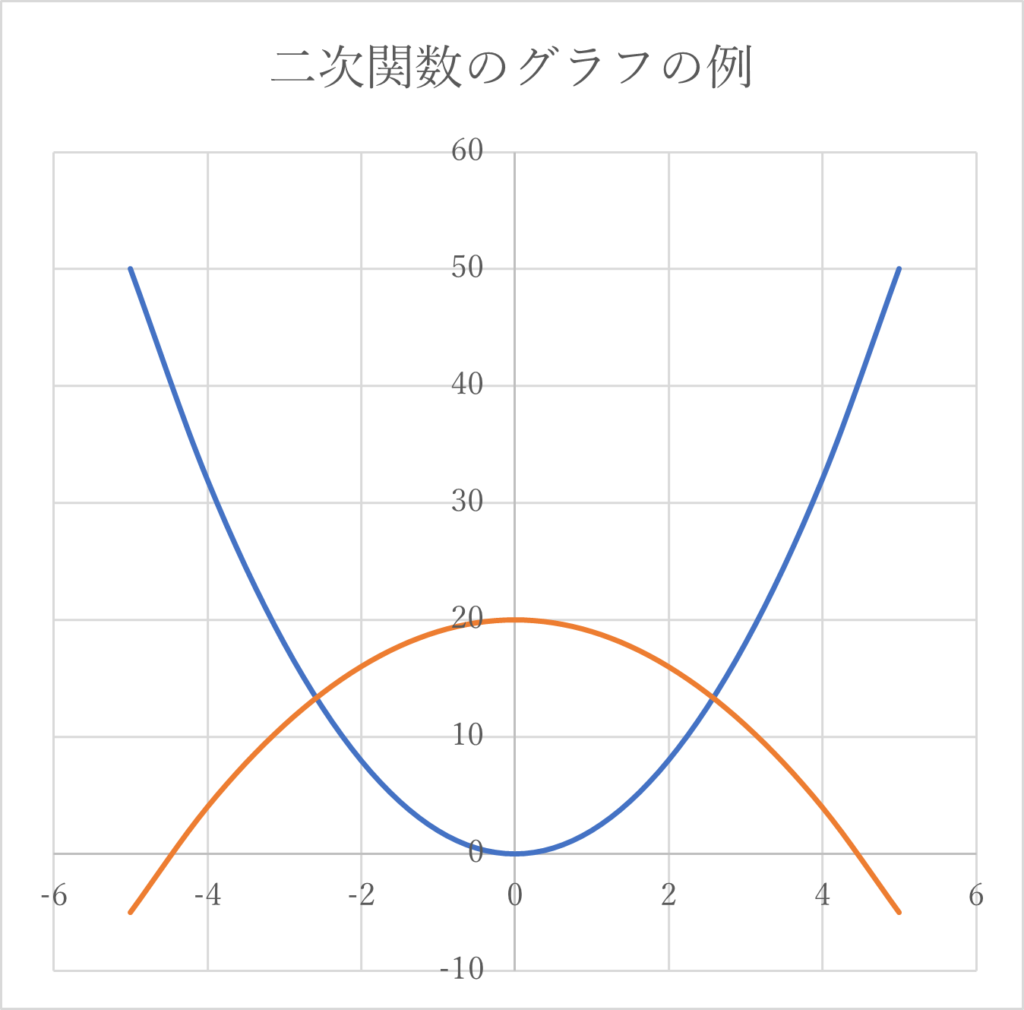
「yがxの関数で、y=2x²+3x－7、y=－3x² のように、yがxの二次式で表されるとき、yはxの二次関数であるという」

 

二次関数は「y=ax²+bx+c, a,b,cは定数」と表すことができます。

とくに中学校で習うy=ax²の形のものは二乗に比例する関数とも呼ばれます。

 

 

y=ax²の解き方の基本

基礎の基礎

式を求める

① y=ax²の式に、わかっているxとyの値を代入してaの値を求めます。

② 求めたaをy=ax²に代入すれば式が完成します。

 

例題：yはxの２乗に比例し、x=2のときy=－20である。yをxの式で表しなさい。

解答：求める式をy=ax²とおく。

x=2、y=－20をy=ax²に代入すると

－20=a×2²

4a=－20

a=－5

求めたaの値をy=ax²に代入して

y=－5x²

 

変化の割合

一次関数の変化の割合は傾き（y=ax+bのaの値）に等しかったので、式さえ分かっていればすぐに答えられましたが、二次関数は一定の値ではなく、aの値と等しいとは限りません。

変化の割合の基本に戻って

を使って計算しましょう。

 

例題：関数y=4x²について、xの値が－6から－3まで増加するときの変化の割合を求めなさい。

解答：x=－6のときのyの値を求める。y=4x²にx=－6を代入して

y=4×(－6)²

y=4×36

y=144

x=－3のときのyの値を求める。y=4x²にx=－3を代入して

y=4×(－3)²

y=4×9

y=36

ｘの増加量は(－3)－(－6)＝3、yの増加量は36－144＝－108となるので

　

 

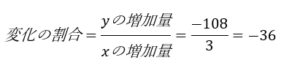
ｙの変域を求める

ｘの変域が与えられたときにｙの変域を求める問題では注意が必要です。

一次関数ではｘの変域の最小値と最大値をそれぞれ式に代入して小さい順に並べれば答えとなりましたが、y=ax²ではそうならない場合があります。確認していきましょう。

 

(1)xの最大値と最小値が同符号の場合

xの変域が 3≤x≤8 や －9≤x≤－2 のように同じ符号の範囲で変域が与えられているときは、一次関数のときと同様の方法で求めることができます。

 

例題：関数y=2x² のx変域が次のとき、y変域を求めよ。

１）3 ≤x≤5          2）－4≤x≤－1

解答：１）x=3 のときのyの値を求める。y=2x² にx=3 を代入して

y=2×3²

y=2×9

y=18

x=5のときのyの値を求める。y=2x²にx=5を代入して

y=2×5²

y=2×25

y=50

よって、ｙの変域は18≤y≤50

２）x=－4のときのｙの値を求める。y=2x² にx=－4 を代入して

y=2×(－4)²

y=2×16

y＝32

x=－1のときのyの値を求める。y=2x² にx=－1 を代入して

y=2×(－1)²

y=2×1

y=2

よって、yの変域は　2≤y≤32

 

(2)xの最大値と最小値が異符号の場合

xの変域の最大値と最小値が異なる符号の時は、必ずyの変域の最大値と最小値のどちらかが0となります。

もう一方の値は絶対値の大きな値を代入したほうの値が採用されます。

 

例題：関数y=2x²のx変域が－3≤ｘ≤5 のとき、y変域を求めよ。

解答：x変域の最大値がプラスの値で最小値がマイナスの値になっているので、 y変域のどちらかの値は０となる。もう一方の値は絶対値が大きいほうの値を代入した値が採用されるので、今回の問題では －3と5では 5のほうが絶対値の値が大きい。よってx=5 を代入して yの値を求める。

y=2x²にx=5 を代入して

y=2×5²

y=2×25

y=50

よって、yの変域は0≤y≤50

 

グラフの書き方

y=ax²のグラフを書く手順

① 原点に点を打つ

② x=1,x=2,x=3,…を式に代入してyの値を求めて、点を打つ（yが分数になるときは点を打たない）

③ ②の点とy軸に対称な点を打つ

④ 点を滑らかな曲線でつなぎ、グラフ用紙の端までのばして書く

 

例題：　　 のグラフを記入しなさい

 

① 原点に点を打ちます

 

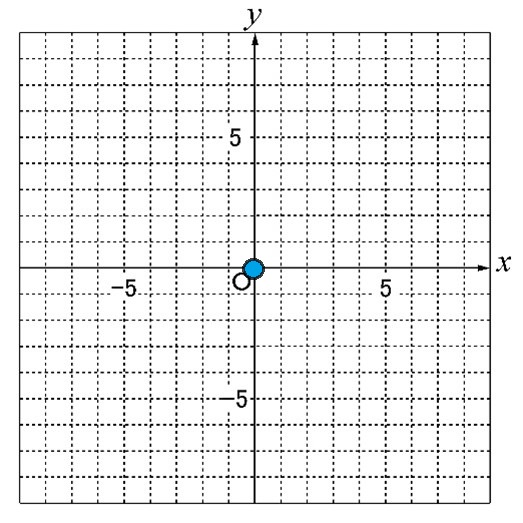
② 整数の値になるx=2,x=4,x=6 のときの点をうちます

 

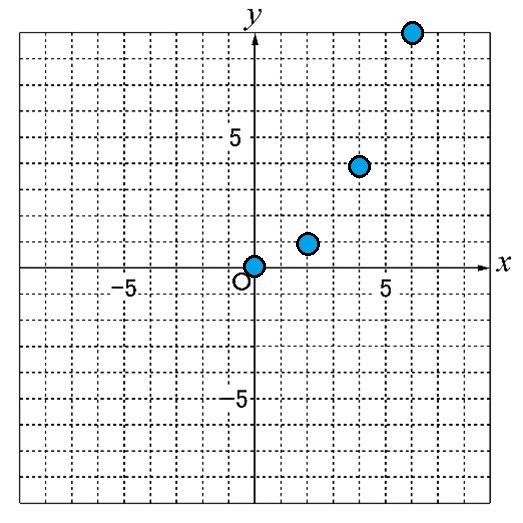
③ ②の点とy軸に対称な点をうちます

 

 

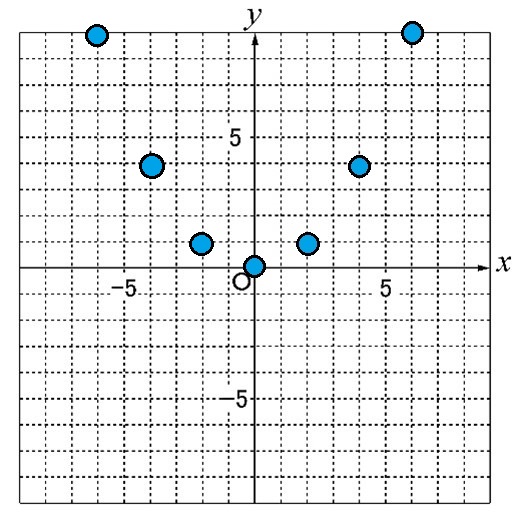
④ 点を滑らかな曲線でつなぎ、グラフ用紙の端までのばして書きます

 

 

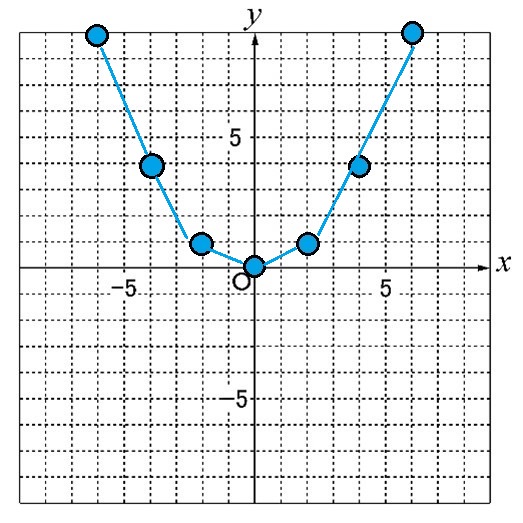
関数 y=ax²の利用

〇制動距離

自動車のブレーキがききはじめてから停止するまでの距離を制動距離といいます。

制動距離は、自動車の速さの2乗に比例するという関係があり、これを利用した問題が出題されます。

 

例題：制動距離は、車の速さの2乗に比例するという。ある車が時速50キロメートルで走っているときの制動距離を25メートルとする。

① 時速xキロメートルの時の制動距離をyメートルとして、xとyの関係を式に表しなさい。

② 時速60キロメートルのとき、制動距離は何メートルになるか。

③ 制動距離が49メートルになるのは、時速何キロメートルのときか。

 

解答①

基本の式 y=ax²にx=50,y＝25 を代入してaを求める

y=ax²

25=a×50²

2500a=25

よって、基本の式y=ax²にを代入して

 

解答②

解答①で求めた式にx=60を代入する

 

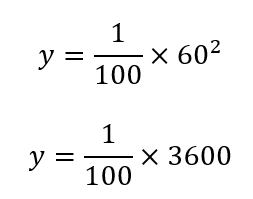
y=36

よって、制動距離は36メートル

 

解答③

解答①で求めた式 にy=49を代入する

x²＝4900

x=±70

x=－70は問題に適さないので、答えは時速70キロメートル

 

 

〇振り子の長さと周期

振り子が1往復するのにかかる時間は、おもりの重さや振れ幅に関係なく一定で、それを周期といいます。

振り子の長さは、周期の2乗に比例する関係があり、これを利用した問題が出題されます。

 

例題：周期が x秒の振り子の長さをyメートルとすると、およそという関係がある。

① 周期が4秒である振り子をつくるには、振り子の長さを何メートルにすればよいか。

② 長さが6.25メートルの振り子の周期は、何秒になるか。

 

解答①

与えられた式に、x=4 を代入すると

 

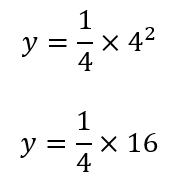
y=4

よって、振り子の長さは4メートルにすればよい

 

解答②

与えられた式に、y=6.25 を代入すると

x²=25

x=±5

x=－5は問題に適さないので、振り子の周期は5秒

 

二次関数の公式

二次関数に関する公式は頂点の座標を求めるものや判別式がありますが、今回の範囲ではないのでここでは省略します。

ただ、変化の割合については公式がありますので確認していきましょう。

 

公式：y=ax²において、xの値がからまで増加するとき、

 

例題：y=4x²について、 xの値が－6から－3まで増加するときの変化の割合は

＝４{(－6)＋(－3)}

＝4×(－9)

＝－36

 

まとめ

今回確認したのは、二次関数の中でも中学校で習う y=ax²（2乗に比例する関数）までの範囲です。

高校で習う範囲ではグラフの頂点の位置が原点からずれており、より複雑なものとなっています。

まずは、今回確認した内容をしっかりと身に着けて、より高いレベルの問題にも対応できるように頑張ってください。