連立不等式の解き方

こんにちは!オンライン家庭教師WAMです(^^)/
今回は連立不等式を解くコツについて詳しく解説していきます。
Contents
基本の連立不等式の解き方
連立不等式の基本の解き方は一次不等式と同じです。
まずは、与えられた不等式をそれぞれで解いていきます。
例題を見ていきましょう。
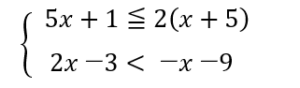
それぞれの式をまずは別々に計算していきます。
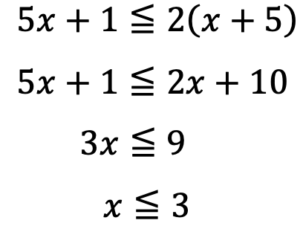
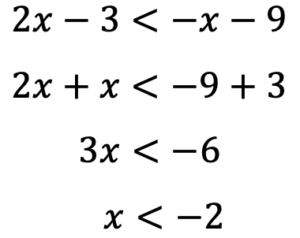
次にそれぞれの解の範囲について考えます。
頭の中で考えてもよいですが慣れないうちは数直線上に解を表してみましょう。
x≦3かつx<-2の範囲は
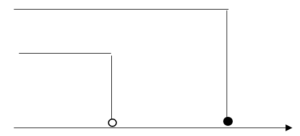
–2 3 x
上の数直線で重なっている範囲は x<-2。
この〈x<-2〉が答えはとなります。
ポイントとしては
①まずは別々に不等式を解く
②解の範囲が重なる範囲を考える
この2つになります!!
では、例題を何問か解いていきましょう。
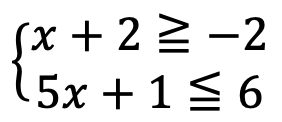
同じ手順で考えていきましょう。
まずは別々に不等式を解いていきます。
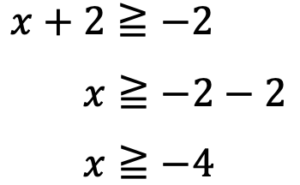
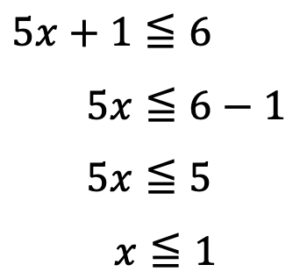
これらの解の共通の範囲を考えると
![]()
となります。
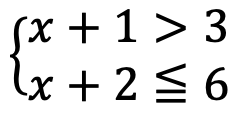
それぞれの不等式を解いていくと
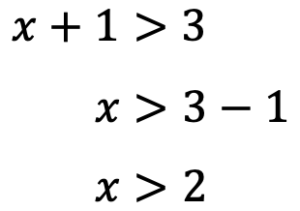
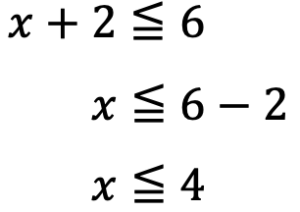
これらの解の範囲を考えると
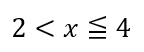
不等式のポイントとしては1つの解がバシッと決まるのではなく解の範囲がわかるという点です。
それぞれの解の範囲を求めたうえで解の共通の範囲を求めていきましょう。
連立不等式で注意すること
連立不等式の解き方は理解していただけましたか?
ここからは連立不等式において注意すべき事項について説明していきます。
解なしの場合
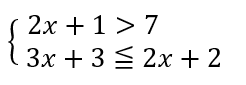
まずはそれぞれの不等式を解いていきます。


これらの解を図に表してみましょう。
![]()
![]()
-1 3 Χ
この図の共通な部分を考えると共通範囲は「ない」ことがわかります。
この場合は、答えは「解なし」となります。
3つ辺を持つ不等式
![]()
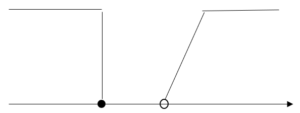
このような不等式の場合は左2つと右2つの不等式に分けて考えていきます。
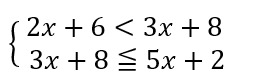
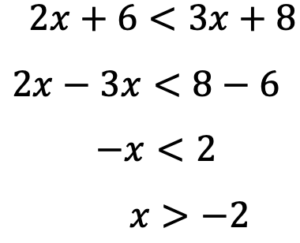
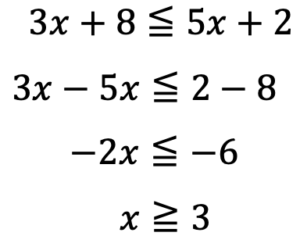
この時に<なのか≦なのか注意しておきましょう。
この2つの範囲を考えていくと
-2 3 Χ
これらの解の範囲を考えると
![]()

解がすべての実数?!
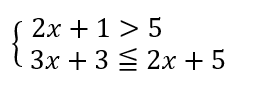
この連立不等式を解いていきましょう。
まずはそれぞれの不等式を解いていきましょう。
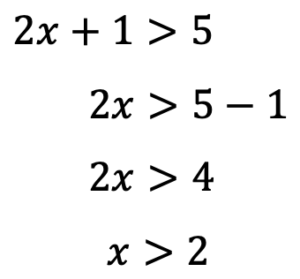
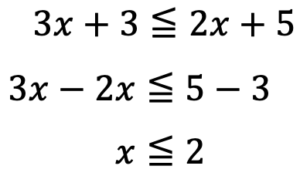
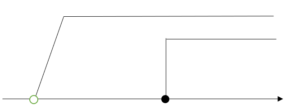
この解を数直線に表してみましょう。
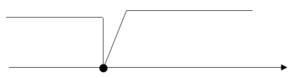
2 Χ
この解の範囲を考えると実数全部になります。
この場合、解は「すべての実数」になります。
この場合も不安にならずに自信をもって解答しましょう。
様々な連立不等式
ここからは連立不等式の様々な問題について学習していきましょう。
不等式中の定数を求める問題
aを定数としたときに次の連立不等式
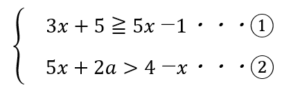
を同時に満たす整数が存在し、かつそれが自然数になる時のaの範囲を求めよ。
まずは①を解いてみます。
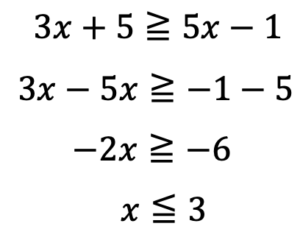
次に②を考えてみると
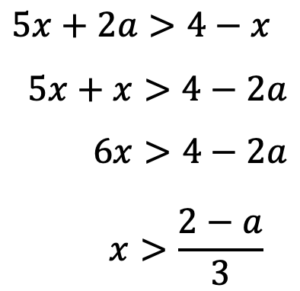
この範囲を数直線上に表してみましょう。
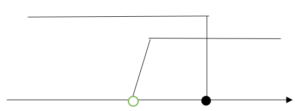
(2-a)/3 3 Χ
この点が動く
①と②が共通の自然数の解を持つ場合について考えます。
上の図を見ると①と②が共通範囲を持つような実数aの条件はこの範囲が0以上であり3を超えない範囲にあることなので、
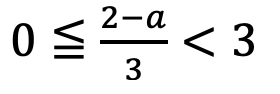
この式を解くと
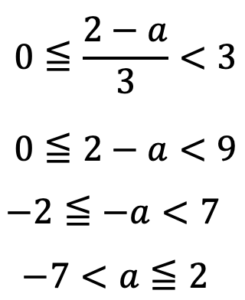
となります。
具体的に数直線に書き出すことがポイントになります。
分数・()を含む連立不等式

分数を含む不等式は、まずは両辺に最小公倍数をかけて整数のみの不等式にしましょう。
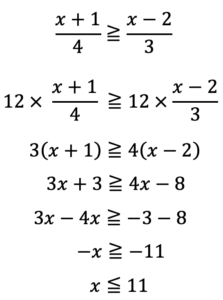
②の不等式も解いてみましょう。
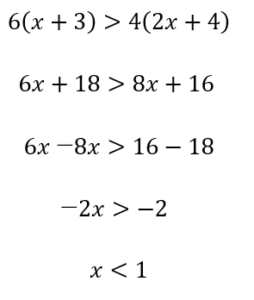
この2つの不等式の共通の解は
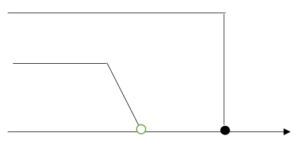
1 11 Χ
上の図からわかるように共通の解はx<1となります。
最後にもう一問解いてみましょう。
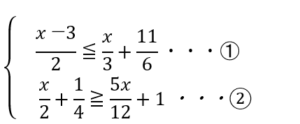
この場合も同様に考えていきましょう。
まずは①を解いてみます。
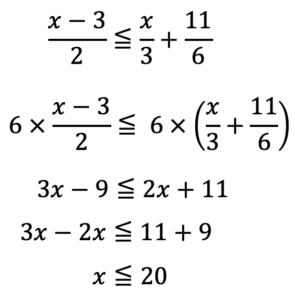
次に②を考えてみると
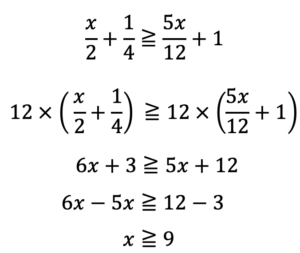
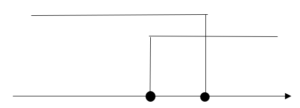
9 20 Χ
これらの解の範囲を考えると
![]()
様々な問題がありますがどの問題においても基本は同じになります。
それぞれの不等式を解いてその後数直線上で共通の範囲を求めるのがポイントです。

まとめ
ここまで連立不等式について解説してきましたがいかがでしたか?
基本事項は一次不等式の解き方と何も変わりません。
連立不等式で重要なのは共通の範囲をイメージできるかです。
共通の範囲を数直線を用いて具体的にイメージすることで計算ミスをなくしていきましょう。
■ この記事の監修者

オンライン家庭教師WAM講師。小・中は全科目対応。高においても国・数・英・物・化・地理と幅広く対応可。
受験生時代は浪人を経験し、その挫折経験が生徒への親身な対応に繋がっている。大学に入ってからも勉強することを怠らず、専門領域以外の知識をも身に付けている。その幅広い教養から繰り出される授業は必見・必聴。















