一次不等式について学ぼう 

こんにちは！オンライン家庭教師WAMです\(^^)/

 

一次方程式は解けるけど、不等式になるとちょっと難しい…
不等号が入っていると何となく難しそうな印象を持つ人もいるのではないでしょうか。
今回は、不等号を使った計算式である「不等式」について詳しく解説していきたいと思います！

 

 

一次不等式の解き方

一次不等式の解き方

まず、一次不等式はどのように解くのかについて解説していきます。

 

この時使う不定式の性質は

・不等式の両辺に同じ数を足しても引いても、不等式の関係は変わらない
・不等式の両辺に同じ正の数をかけたり割ったりしても、不等式の関係は変わらない
・不等式の両辺に同じ負の数をかけたり割ったりすると、不等号の向きが変わる

 

この性質を利用して不等式を解いていきます。

 

一次不等式の解き方の基本は、「一次方程式」の解き方です。
基本的には、移項して左辺に文字、右辺に数字を集めていきます。

 

では例題を一緒に解いていきましょう。

 

まずは文字を含むものを左辺に、文字を含まないものを右辺に移項していきます。

 

 

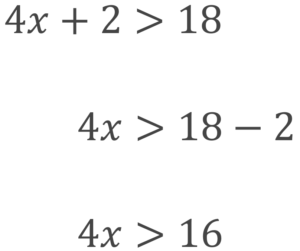
次に両辺を４で割っていきます。

 

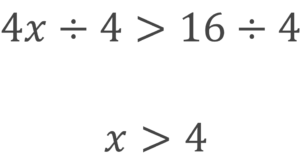
答えはx>4になります。
基本的には、方程式と同じように解いていきます。

 

 

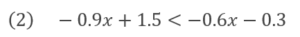
この場合は小数によって計算がややこしくなるのを避けたいので全体を10倍します。

 

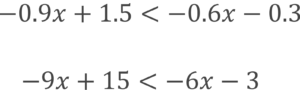
ここで⑴と同様に左辺に文字、右辺に数字を集めるように移行していきます。

 

 

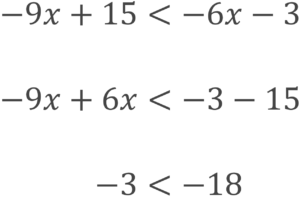
ここで両辺を-3で割っていくのですが、『不等号の向き』に注意が必要です。
負の数で両辺を割る時は不等号の向きが変わります。

 

 

答えはx>6になります。
負の数が関わってくると計算ミスがぐっと増えるので、注意して計算するようにしましょう。

 

 

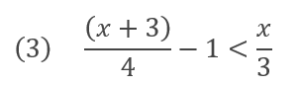
分数が絡む問題は、最小公倍数を両辺にかけて整数のみの式にしたうえで計算するようにしていきましょう。
この場合は「4」と「3」の最小公倍数なので、「12」をかけることで整数のみの式に直すことができます。

 

 

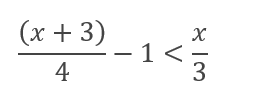
両辺に12をかけます。

 

 

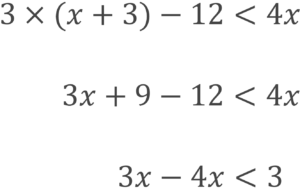
左辺に文字、右辺に数字を移項します。

 

両辺に-1をかけます。この時、不等号の向きに注意しましょう。

 

 

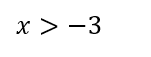
練習問題

練習問題を何問か解いてみましょう。

 

 

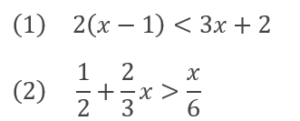
基本に則って解くことで、答えを導くことができると思います。

 

 

 

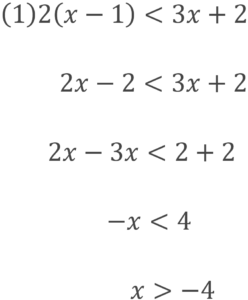
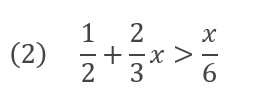
両辺に6をかけます。

 

 

 

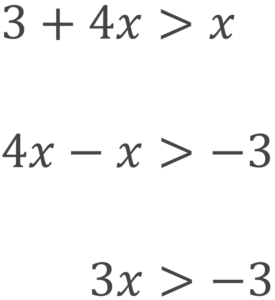
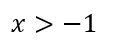
一次不等式の解と数直線

次に一次不等式と数直線の関係について学んでいきましょう。

 

数直線とは、直線上の点と実数を対応させて視覚的にとらえる考え方です。
不等式の解をより分かりやすく理解することができます。
例えば、《 x < 1 》のように、一次不等式の解は一点ではなく「範囲」となるため、ちょっとした工夫が必要です。

 

数直線上で範囲を表す場合は以下のように表現します。

 

 

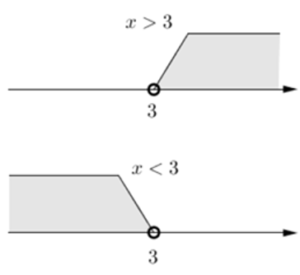
上の図では、答えは3より大きい範囲を示しています。
ポイントは3の点が○（白い丸）になっているので3を含みません。
3より小さい範囲を示すときは、下の図のように左側に線を伸ばします。

 

では、3を含む場合はどのように表すのでしょうか。
その場合は、●（黒い丸）で表します。

 

 

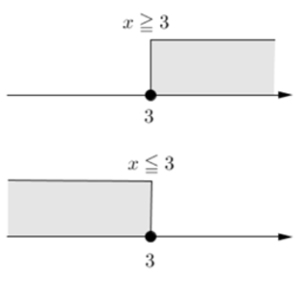
この場合は、3を含むので境目の直線を垂直に書くことが多いです。

 

この基本をおさえれば、複数の範囲を同時に考えることも可能です。

 

 

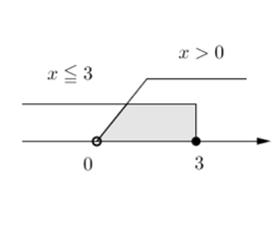
このように、数直線上で複数の範囲を書き表すことで、両方の条件を満たす範囲を視覚的にとらえることができます。

 

上の図では式で表すと

 

 

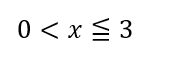
となります。

 

連立不等式を考える場合は、この考え方が役に立つので今のうちに慣れておきましょう。

 

 

応用問題に挑戦してみよう

代金の問題

まずは基本的な文章問題を解いていきましょう！

 

1冊120円のノートと1つ80円の消しゴムを合わせて、10個買ってその代金を1000円以内にしたい場合を考えます。
ノートの冊数をできるだけ多くしたいとき、それぞれいくつずつ買うことができるか求めなさい。

 

ノートの冊数をx冊とします。
この時のポイントは、消しゴムを(10–x)個と表現できるということです。

 

これらを用いると代金は

 

 

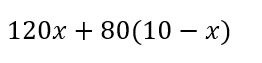
と表すことができます。

 

この代金が1000円以下になればよいので、不等式は

 

 

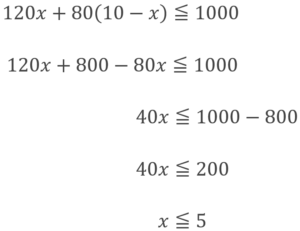
できるだけ多くノートを買いたいのでノートは5冊、消しゴムは5個が答えになります。

 

絶対値のついた一次不等式

下記の問題を解きなさい。

 

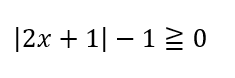
絶対値の中身が、正なのか負なのかによって場合分けしていきます。

 

 

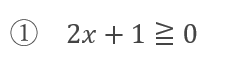
の時 、つまり

 

 

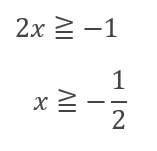
この時、絶対値を外しても符号は変化しないので

 

 

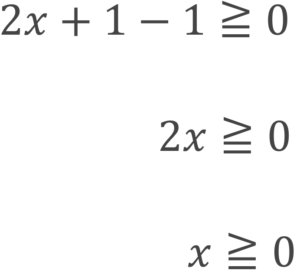
と求めることができます。

この解は、下記を満たします。

 

 

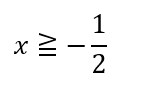
次に、

 

 

の時、つまり

 

 

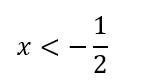
絶対値を外すと、符号は変化するので

 

 

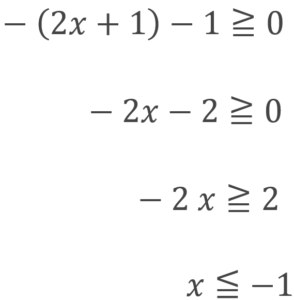
この解は、下記を満たします。

 

 

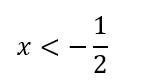
よって、①②の解から

 

 

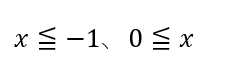
と求めることができます。

 

応用問題なので、少し難しかったですね。

 

条件を満たす自然数を求める問題

 

 

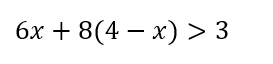
を満たす2ケタの自然数をすべて求めよ。

 

まずは一次不等式を解いていきましょう。

 

 

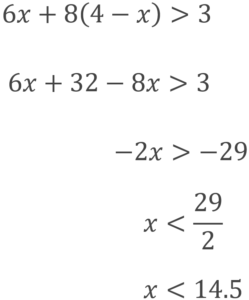
この式を満たす2ケタの自然数は、「10、11、12、13、14」になります。

 

分かりにくい場合は数直線を書いてみるのもよいと思います。

 

文章問題

4％の食塩水と10％の食塩水がある。4％の食塩水200 gと10％の食塩水を混ぜて、6％以上の食塩水を作りたい。
この時、10％の食塩水は最低何g必要か？

 

文章問題では、状況を理解する能力が必要になってきます。

1つ1つの条件を式に表していきましょう。

 

10％の食塩水の量をx gとする。

食塩水の問題のポイントは、「食塩水全量、水の量、食塩の量のどれに着目するか」です。

 

また、濃度は「食塩の量/食塩水の量」で表されます。

 

 

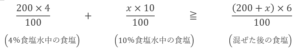
この式を計算していきましょう。

 

 

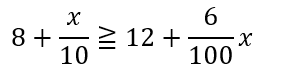
式全体を100倍すると

 

 

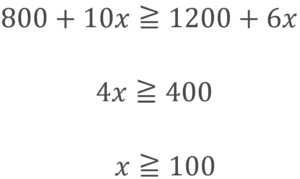
よって、10％の食塩水は最低でも100g必要になります。

 

状況をしっかり式に表すことができれば、あとは一次不等式を解くだけです。
この時、不等号の向きなどの計算ミスに注意しましょう。

 

 

まとめ

今回は一次不等式について紹介してきましたが、理解は深まりましたか？
一次方程式をしっかり理解できていれば、あとは符号の向きに注意するだけです。
応用問題は少し難しめだったので、解けなくても落ち込む必要はありません。
苦手意識をもたずに応用問題にどんどん挑戦していきましょう。