教えて！鶴亀算の解き方

こんにちは！オンライン家庭教師WAMです(^^)/

 

突然ですが、皆さんは「鶴亀算」という言葉を聞いたことがありますか？

実は「旅人算」「流水算」「仕事算」「分配算」「通過算」のような言葉と同じように、

学校では習わない、少し特殊な算数の文章問題の事を表しています。

恐らく、今までで一度は聞いたことがあるよ、という方が多いのではないでしょうか。

特に、中学受験を経験される方に関しては、避けては通れない文章問題となっています。

 

今回は「鶴亀算」に焦点を当てて、解き方を説明していきたいと思います。

 

 

そもそも鶴亀算（つるかめざん）って何？？

 

 

例えばですが、「カメが10匹います。足は合計で何本ありますか？」という問題があるとしましょう。カメの足は4本なので、皆さんは40本と正解を導き出すことが出来るかと思います。

式　10×4=40　答え40本

 

では、「カメが何匹かいます。足は合計で52本あります。カメは合計で何匹いますか？」

これも簡単に、13匹と答えられると思います。

式　52÷4=13　答え13匹

 

続いて、「ツルが何羽かいます。足は合計で28本あります。ツルは合計で何羽いますか？」

きっと皆さんは余裕で14羽と答えると思います。

式　28÷2=14　答え14羽

 

では最後に、「ツルとカメが合計で25匹います。足は合計で62本あります。ツルとカメはそれぞれ何匹ずついますか？」

 

「え？？？」

 

となりませんか？？

最初の2問までは、暗算でも答えを出すのは簡単だったと思います。

 

しかしながら、この問題は今までの問題とは全く考え方が違うと気づいた方も多いのではないでしょうか。

そうです、ツルとカメは1匹の足の数が異なっている為、全て一緒に計算するという事が出来ないのです。

このように総数は分かっているが、それぞれの数が分からない問題が「鶴亀算」であり、

他には、代金の違う商品を同時に購入する文章問題なんかも「鶴亀算」に分類されます。

中学受験においては、当たり前のようにこのような問題が出てきますので、受験予定の方は当たり前のように解けなければなりません!!!

 

鶴亀算（つるかめざん）のやり方

 

では、

「ツルとカメが合計で25匹います。足は合計で62本あります。ツルとカメはそれぞれ何匹ずついますか？」

という問題を、どう考えたら良いのかという事ですが、まずは様々な解き方を見ていきましょう。

 

グラフで考えるやり方

先程の問題では、ツルとカメの合計が25匹ということなので、このようにグラフにして考えてみると・・・

 

 

ツルが25匹だと足が50本、カメが0匹だと足が0本で　合計が50本

ツルが24匹だと足が48本、カメが1匹だと足が4本で　合計が52本

ツルが23匹だと足が46本、カメが2匹だと足が8本で　合計が54本

ツルの数が1減り、カメの数が1増えると、足の合計が２ずつ増えることが分かります。

 

ツルが19匹、カメが6匹の時、足の合計が62本となりますので、これが正解となります。

 

原始的な解き方ではありますが、これが根本的な考え方となります。

 

 

面積で考えるやり方

では次に、面積を使って考える方法を見てきましょう。

「ツルとカメが合計で25匹います。足は合計で62本あります。ツルとカメはそれぞれ何匹ずついますか？」

 

 

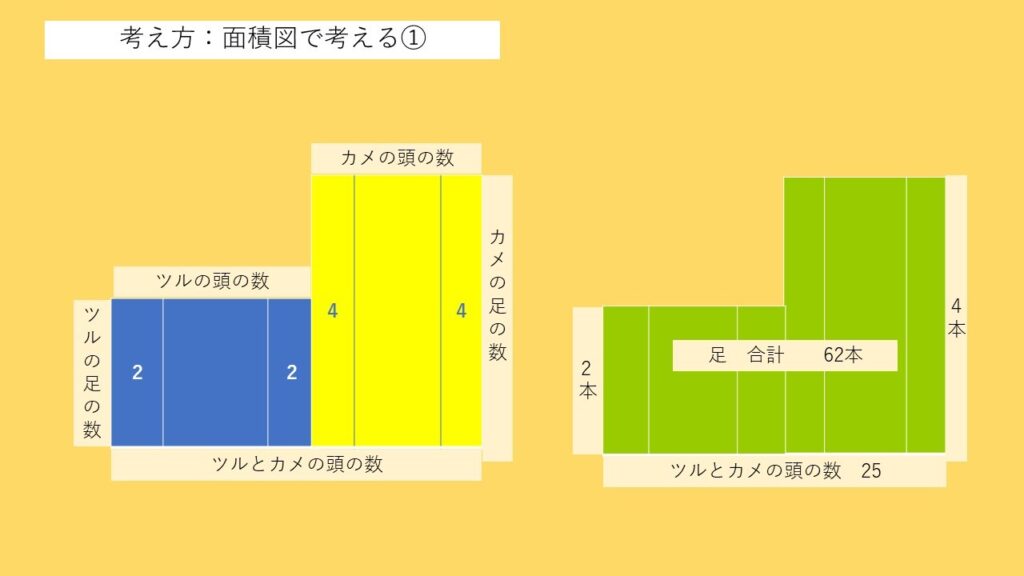
ツルとカメの足の数を面積として、長方形を使って表しますが、

 

①横の長さはツルとカメの頭の数

②縦の長さはツルとカメの足の数

③面積はツルとカメの足の合計の数

 

このようにして面積の図を書いてみましょう。

図を描いた後は、全部ツルだった場合、全部カメだった場合という考え方で解いていきます。

 

＜全部ツル、全部カメで考える＞

・全部ツルの場合

・全部カメの場合

に分けて解き方を見ていきましょう。

 

 

・全部ツルの場合

 

 

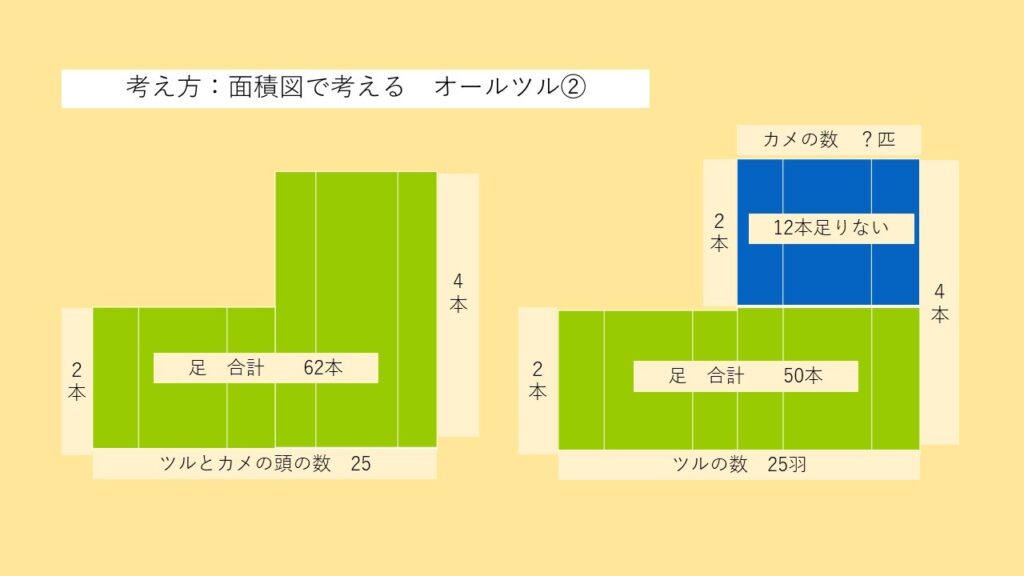
全部ツルとして考えた場合、足の数は50本しかありませんので、合計の足の数の62本から、足が12本不足している事になります。

ここからツルが1匹減り、カメが1匹増えた場合は足が2本ずつ増えるため、

 

→　12（不足している足の数）÷2（増える足の数）＝6匹（カメの数）

 

これでカメが6匹いるという事が分かり、

 

→　25（ツル、カメの合計数）－6（カメの数）＝19匹（ツルの数）

 

このように簡単にツルの数とカメの数を求めることが出来ます。

 

 

 

・全部カメの場合

 

 

同じように、全部カメとして考えた場合、足の数は100本となり、合計の足の数の62本から、足が38本多くなってしまいます。

ここからツルが1匹増え、カメが1匹減った場合は足が2本ずつ減るため、

 

→　38（多くなる足の数）÷2（減る足の数）＝19匹（ツルの数）

 

これでツルが19匹いるという事が分かり、

 

→　25（ツル、カメの合計数）－19（ツルの数）＝6匹（カメの数）

 

このように、どちらの場合でも簡単にツルの数とカメの数を求めることが出来ます。

 

 

実際に鶴亀算（つるかめざん）の問題を解いてみよう

ではここからは、実際にいくつかの問題を解いてみましょう。

 

問題1

1個150円のりんごと1個280円の桃を合計で12個購入したところ、合計金額は2320円となった。購入したりんごと桃の個数を答えよ。

 

 

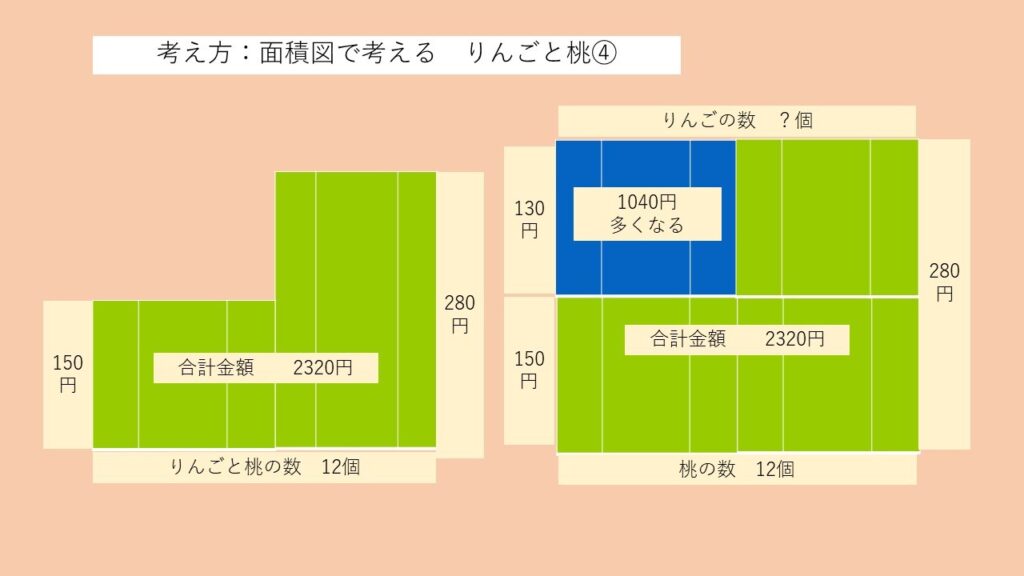
この問題に関しても、面積の図を書いて考えてみましょう。

12個全て桃を購入したと考えた場合、3360円となりますので、合計金額の2320円よりも1040円多い事になります。

桃が1個減り、りんごが1個増えた場合、桃とりんごの金額の差は130円となるため、

 

→　1040÷130＝8個（りんごの数）

 

これでりんごの数が8個だと分かり、

 

→　12－8＝4個（桃の数）

 

答え　りんご8個　桃4個

 

 

問題２

１本80円の鉛筆と1本130円のボールペンを合計17本買い、2000円支払ったところ、おつりは240円であった。購入した鉛筆とボールペンの本数をそれぞれ答えよ。

 

 

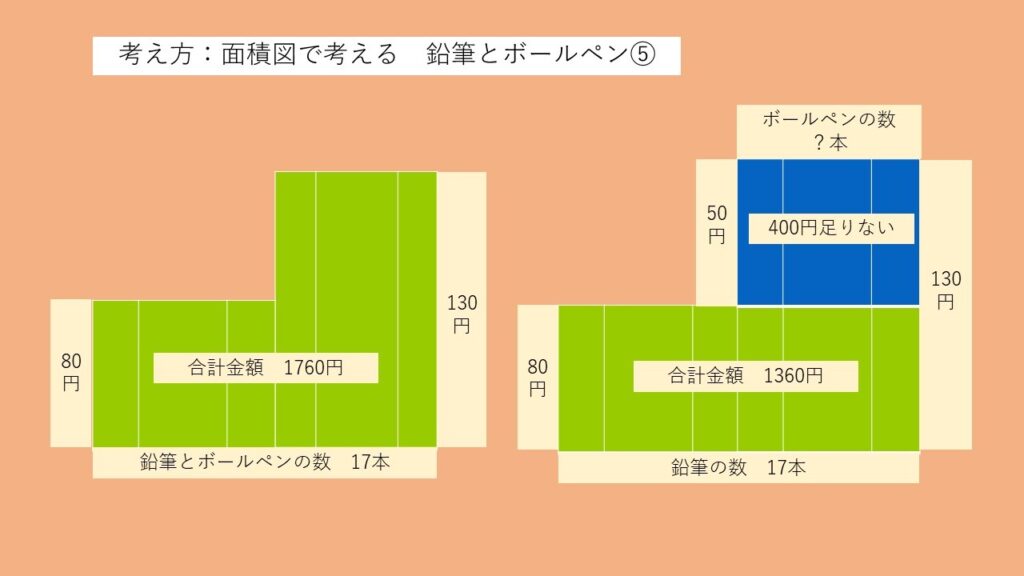
この問題に関しては、まずは鉛筆とボールペンの合計金額を計算してから、面積の図を書きましょう。

 

→　2000－240＝1760円（鉛筆とボールペンの合計金額）

 

17本全て鉛筆を購入したと考えた場合、1360円となるため、合計金額1760円と比べると400円不足していることになります。

鉛筆が1本減り、ボールペンが1本増えた場合、金額の差は50円となるため、

 

→　400－50＝8本（ボールペンの本数）

 

これでボールペンの本数が8本だと分かり、

 

→　17－8＝9本（鉛筆の本数）

 

答え　鉛筆9本　ボールペン8本

 

 

鶴亀算（つるかめざん）で間違いやすいポイント

必ずしも鶴と亀が登場するわけではない

勘違いする方がたまにいらっしゃいますが、『鶴亀算は必ずしも、鶴と亀が登場し、その頭数を計算するという問題ではない』ということです。

 

時間や物の個数など、様々な問題パターンが存在します。

『2種類のものの合計がわかっている場合に鶴亀算を使用する』ということを覚えておきましょう。

 

 

まとめ

「鶴亀算」の解き方、少しでも分かるようになりましたか？？

中学受験には、このように学校では習わない様々な難しい文章問題が出題されます。

色々な形式の問題を練習し、たくさん解けるようになれば、皆さんが受験したい志望校に合格できる可能性がどんどん高くなっていきますので、これからも頑張ってたくさん練習していきましょう！！！